Bu belge İstatistik hakkında temel kavramlar ve bazi örnekleri içermektedir. Kaynak göstermek koşulu ile alıntı yapılabilir.
| © Cahit Cengizhan 2001-2003 Ders Notları Arşivinden |
3.2. Değişim (dağılım) Ölçüleri :
3.3. Verilerin Sınıflandırılması
3.4. Gruplanmamış veriler için örnek:
3.5. Gruplanmış veriler için örnek:
6.1. PARAMETRİK HİPOTEZ TESTLERİ:
6.1.1.Tek Ana Kütle Ortalaması Hipotez Testi ( Bağımlı gruplarda T Testi)
6.1.2. Tek Ana Kütle Oranı İle İlgili Hipotez Testi
6.1.3. İki Örnek Ortalamasının Karşılaştırılması (Bağımsız gruplarda T testi)
6.1.4. İki Örnek Oranının Karşılaştırılması:
6.1.5. Varyans Analizi ( F Testi )
Değişken: Gözlemden gözleme değişik değerler alabilen objelere, özelliklere ya da durumlara "Değişken" denir.
Nicel (Kantitatif) Değişken: Değişik derecelerde az ya da çok değerler alabilen değişkendir. Yaş, ağırlık, zeka seviyesi, hava sıcaklığı, hız, nüfus vb.
Nitel (Kalitatif) Değişken: Bu değişkenler gözlemden gözleme farklılık gösterirler, ancak bu farklılık derece yönünden değil kalite ve çeşit yönündendir. Cinsiyet, medeni durum, göz rengi, din, milliyet vb.
Süreksiz Değişken: Bu değişkenler miktar yönünden değişiklik yerine tür yönünden değişiklik gösterir. Dolayısıyla bir obje ya da birey bir özelliğe sahiptir ya da değildir. Cinsiyet, medeni durum gibi. Birinin diğerine göre daha çok veya az olması mümkün değildir. Nitel değişkenlerin hemen hepsi süreksiz dğişkendir.
Sürekli Değişken: İki ayrı ölçüm arası kuramsal olarak sonsuz parçaya bölünebilir. Yaş, uzunluk ve ağırlık gibi.
Ölçme: Objelere ve ya bireylere, belirli bir özelliğe sahip oluş dereclerini belitmek için, belirli kurallara uyarak sembolik değerler verme işlemidir.
Nominal (Sınıflama): Rakamlar sadece verileri farklı gruplara ayırmada kullanılır. Veriye verilen sayı o grubun adıdır. Örneğin, futbol takımındaki rakamlar, plaka işaretleri, cinsiyet 0,1 gibi.
Ordinal (Sıralama): Ölçme sonucunda verilen sayısal değerler büyükten küçüğe sıralanabilir. Bir özelliğe sahip oluş derecesidir. Örneğin, yarışma 1.'si 2.'si 3.'sü, birinci tercih, ikinci tercih vb.
Bu iki ölçek türü ile elde edilmiş verilere genellikle nonparamatrik teknikler uygulanır. Ayrıca parametrik test varsayımları yerine getirilemiyorsa, hangi ölçekle toplanmış olursa olsun nonparamatrik teknikler tercih edilmelidir.
Eşit Aralıklı: Sıfır ile ifade edilen bir başlangıç noktası olan, sıfırın yokluğu göstermediği kabul edilen ölçektir. Örneğin, termometre ve likert ölçeği gibi.
Oranlı: Gerçek sıfır değerine sahip ve sıfır yokluğu ifade eden birbirinin katı olarak ifade edilebilen ölçek türüdür. Metre, kg. gibi.
İstatistikte kullanılan bazı parametreler ve simgeleri:
| Örneklem Parametresi | Evren Parametresi | |
| Aritmetik ortalama | X | µ |
| Standart sapma | S |
s |
| Varyans | S2 | s2 |
| Birey (Gözlem)sayısı | n | N |
| Korelasyon | r | j |
Aritmetik ortalama: Deneklerin aldıkları değerlerin toplanıp denek sayısına bölünmesiyle elde edilen değerdir.
Ortanca: Bir ölçek üzerinde orta noktanın yerini gösteren bu ölçü tüm değerleri ortadan ikiye bölen değerdir.
Mod: Ölçümlerde en fazla tekrar edilen değere mod denir.
Ranj: En büyük ölçümle en küçük ölçüm arasındaki farktır.
Standart sapma: Ölçümlerin ortalamadan olan farklarının karelerinin ortalamasının kareköküdür.
Standart hata: Aritmetik ortalamada oluşan hatanın belirlenmesi için bulunur.
Bir işletmenin yaptığı üretim belirli bir zaman diliminde ölçülmüş ve aşağıdaki veriler elde edilmiştir.
| 115 |
94 |
110 |
103 |
92 |
104 |
114 |
106 |
100 |
102 |
100 |
95 |
97 |
113 |
98 |
| 101 |
99 |
103 |
93 |
107 |
96 |
113 |
110 |
108 |
102 |
114 |
90 |
100 |
103 |
114 |
| 111 |
105 |
99 |
102 |
98 |
97 |
93 |
91 |
99 |
114 |
108 |
103 |
100 |
98 |
101 |
| 104 |
110 |
114 |
113 |
109 |
108 |
106 |
115 |
103 |
111 |
109 |
112 |
104 |
104 |
102 |
| 107 |
106 |
119 |
105 |
96 |
94 |
96 |
101 |
101 |
106 |
107 |
105 |
113 |
112 |
99 |
1. Dağılımdaki en büyük ve en küçük değer bulunur. Örneğimizdeki en büyük değer 115, en küçük değer 90'dır.
2. En büyük değerden en küçük değer çıkarılarak dağılım aralığı bulunur.
Dağılım aralığı = En büyük değer- En küçük değer Dağılım aralığı= 115-90=25
3. Dağılım aralığı bir kez 8'e bir kez 15'e bölünerek(sınıf sayısının en az 8, en çok 15 olmasını önerdiğimiz için) sınıf aralığı saptanmaya çalışılır. 25÷8=3.1, 25÷15=1.6'dır. 1.6 ile 3.1 arasında herhangi bir değer sınıf aralığı olarak seçilebilir. Eğer sınıf aralığını 3 olarak alırsak yaklaşık 8-9 sınıf elde ederiz, sınıf aralığını 2 alırsak sınıf sayımız 12-13 arasında olur. Burada sınıf aralığı 3 olarak alınmıştır. Sınıflar şu şekilde olur:
Sınıflar
90-92
93-95
96-98
99-101
102-104
105-107
108-110
111-113
114-116
En küçük değer 90 olduğundan ilk sınıfın alt sınırı 90 ile başlatılmıştır. Tüm sınıf sayımız ise 9'dur. Bütün değerler sınıflamaya dahil edilmiştir.
Her Sınıfa Düşen Frekans (Sıklık)
Sınıflar saptandıktan sonra her bir değerin hangi sınıfa gireceğine bakılır. Örneğimizdeki ilk değer 115'dir. Bu değer 114-116 sınıfına gireceği için bu sınıfın karşısına bir çizgi çizilir. Sonra geri kalan değerler teker teker ait oldukları sınıfın karşısına işaretlenir. Buna "Çetereleme" denir. Sonra çeteleler sayılır ve her sınıfın karşısına yazılır. Örnek dağılımımızın çetele ve sayı ile gösterilmesi şöyledir:
| Sınıflar |
Çetele |
Frekans |
| 90-92 |
/// |
3 |
| 93-95 |
///// |
5 |
| 96-98 |
///// /// |
8 |
| 99-101 |
///// ///// // |
12 |
| 102-104 |
///// ///// //// |
14 |
| 105-107 |
///// ///// / |
11 |
| 108-110 |
///// //// |
9 |
| 111-113 |
///// /// |
8 |
| 114-116 |
///// |
5 |
| Toplam 75 | ||
Bir işletmedeki yıllık izinler gün olarak aşağıdaki gibidir. 8,8,7,7,7,6,6,5,5,4,4,3 Buna göre;
a) Ortalama izin kaç gündür?
b) Bu grubun ortancası kaçtır?
c) Mod'u kaçtır?
d) Ranj'ı kaçtır?
e) Standart sapması kaçtır?
f) Standart hatası kaçtır?
Çözüm:
a) 8+8+7+7+7+6+6+5+5+4+4+3=70 (äx)
x=äx/n ; x=70/12 = 5.8 = 6
b) Grubun ortancası 6'dır. c) Mod 7'dir. d) Ranj=8-3= 5
e) Standart sapma: Ölçülerin ortalamadan olan farkları bulunur. Farkların karesi alınır ve toplanır. Bulunan değerler formülde yerine konur.
| Değerler | 8 |
8 |
7 |
7 |
7 |
6 |
6 |
5 |
5 |
4 |
4 |
3 |
| Ortalamadan farkı (x-x) | 2+ |
2+ |
1+ |
1+ |
1+ |
0+ |
0+ |
(-1)+ |
(-1)+ |
(-2)+ |
(-2)+ | (-3) |
| Farkın Karesi (xo-x)2 | 4+ | 4+ | 1+ | 1+ | 1+ | 0+ | 0+ | 1+ | 1+ | 4+ | 4+ | 9 |
| Toplam | 30 | |||||||||||
Standart Sapma:
![]()
f) Standart hata:
![]()
| Değerler |
frekans (f) |
toplam frekans (tf) |
orta nokta X0 |
fX0 |
X0-X |
(X0-X)2 |
| 90-92 |
3 |
75 |
91 |
273 |
-13 |
169 |
| 93-95 |
5 |
72 |
94 |
470 |
-10 |
100 |
| 96-98 |
8 |
67 |
97 |
776 |
-7 |
49 |
| 99-101 |
12 |
59 |
100 |
1200 |
-4 |
16 |
| 102-104 |
14 |
47 |
103 |
1442 |
-1 |
1 |
| 105-107 |
11 |
33 |
106 |
1166 |
2 |
4 |
| 108-110 |
9 |
22 |
109 |
981 |
5 |
25 |
| 111-113 |
8 |
13 |
112 |
896 |
8 |
64 |
| 114-116 |
5 |
5 |
115 |
575 |
11 |
121 |
| Toplam |
75 |
7779 |
549 |
Yukarıdaki değerlere göre; a)Aritmetik ortalamayı,b)Ortancayı, c) Standart sapmayı, d) Standart hatayı,
e) Mod ve f) ranjı hesaplayınız.
Çözüm:
a) Aritmetik ortalama ;
b) Ortanca;
|
|
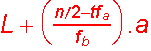 |
L : Ortancanın bulunduğu aralığın alt sınırı
tfa : Ortancanın bulunduğu aralığa kadar toplam frekans
tb : Ortancanın bulunduğu aralığın frekansı
c) Standart sapma;
| Evren | Örneklem |
| |
|
d) Standart hata;
![]()
e) Mod; gruplanmış verilerde en yüksek frekansın bulunduğu aralığın orta noktasıdır. Buna göre mod=103'tür.
f) Ranj = En yüksek değer-en düşük değer Ranj=116-90=2
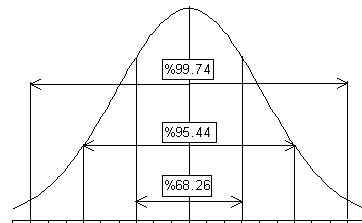
Normal dağılım Özellikleri:
1. Dağılım ortalamaya göre simetriktir. %50'si sağda, %50'si soldadır.
2. Eğriyle X ekseni arasındaki toplam alan 1 birim karedir.
3. Aritmetik ortalama, ortanca, tepe değer(mod) birbirine eşittir.
4. Ortalama ile + - 1 standart sapma arası deneklerin %68.2'sini
Ortalama ile + - 2 standart sapma arası deneklerin %95.44'ünü
Ortalama ile + - 3 standart sapma arası deneklerin %99.74'ünü kapsar.
Bir durum hakkında ileri sürülen varsayımlardır. Önemlilik testleri bir hipotezi test etmek için yapılır. Hipotez, istatistiksel olarak H0 farksızlık hipotezi ve H1 alternatif hipotez olmak üzere gösterilirler.
Öncelikle H0 hipotezi belirlenir. Bu hipotez farksızlığı esas alır. İki ortalama arasında fark yoktur. İki grup arasında ilişki yoktur gibi.
H1 alternatif hipotez ise farklılık üzerine kurulur. H1 hipotezi üç şekilde kurulabilir;
H1 = µ1¹µ2 farklılığı belirten bu hipotez çift yönlüdür.
H1 = µ1>µ2 µ1'in µ2 den büyük olduğunu belirten bu hipotez tek yönlüdür. Sağ kuyruk testi ile test edilir.
H1=µ1<µ2 µ1'in µ2 den küçük olduğunu belirten bu hipotez tek yönlüdür. Sol kuyruk testi ile test edilir.
Bir hipotez kabul veya ret edildiğinde her zaman doğru sonuca varıldığı ya da varılan kararın doğru olduğu söylenemez. Burada iki tip hata ortaya çıkabilir.
| Hipotez |
Kabul etme |
Reddetme |
| Doğru |
Doğru karar |
I. Tip hata (@) |
| Yanlış |
II. Tip hata (ß) |
Doğru karar |
Hipotez: Burs alan öğrenciler almayanlardan daha başarılıdır. Hipotez doğru iken reddedilir ise @ birinci tip hata yapılır. Hipotez yanlış kabul edilirse ß ikinci tip hata yapılır.
Örneklem istatistiklerinden yararlanmak suretiyle bir hipotezin geçerli olup olmadığını ortaya koyma işlemine istatiksel hipotez testi denir.
Parametrik: Ölçümle değer alınmış ve süreklilik gösteren ölçümlere denir. Parametrik testlerde ortalama, varyans, oran gibi ölçüler kullanılır.
Nonparametrik: Verileri sayma veya sıralama şeklinde alınmış değerlerdir. Nonparametrik testler parametrik testlere göre daha zayıftırlar.
1. Verinin ölçüm biçimi, gruptaki denek sayısı, grupların bağımlı ya da bağımsız olması ve varsayımlar dikkate alınarak uygun test seçilir.
2. H0 ve H1 hipotezleri belirtilir.
3. Test istatistiği hesaplanır.
4. Yanılma düzeyi saptanır.
5. Serbestlik derecesi bulunur. (Her teste göre ayrı ayrı hesaplanır)
6. Tablolardan yanılma düzeyi ve serbestlik derecesindeki tablo değeri bulunur.
7. Hesapla bulunan değer ile tablo değeri karşılaştırılır.
8. Karşılaştırma sonucuna göre karara varılarak sonuç @ (anlamlılık) değeri ile birlikte belirtilir.
Hipotez test ederken kullanılan hipotezler aşağıdaki gibi ifade edilir.
| H0 = µ1=µ2 |
H0 = µ1= µ2 |
H0 = µ1=µ2 |
| H1 = µ1 < µ2 |
H1= µ1¹ µ2 |
H1 = µ1>µ2 |
| I. Sol Kuyruk |
II.Çift Kuyruk |
III. Sağ Kuyruk |
Sol kuyruk testinde (I. hipotez grubu): Hesaplanan Z veya t değerleri tablo değerinden küçükse H0 ret H1 kabul, büyük ise H0 kabul H1 ret edilecektir.
Çift yönlü testlerde (II. hipotez grubu): Hesaplanan Z ve t değerleri tablo değerlerinden mutlak değer olarak büyükse H0 ret H1 kabul, küçük ise H0 kabul H1 ret edilir.
Sağ kuyruk testinde (III. hipotez grubu): Hesaplanan Z veya t değeri, bunların teorik değerinden büyük ise H0 ret H1 kabul; küçük ise H0 kabul H1 ret edilecektir.
| Sol kuyruk testi | Çift yönlü | Sağ kuyruk Testi |
|
|
|
|
| Z' nin kritik değerleri önem düzeyine göre aşağıda verilmiştir. |
|||
Önem Derecesi(@) |
Sol Kuyruk Testi |
Sağ Kuyruk Testi |
Çift Yönlü Test |
| 0.10 |
-1.28 |
+1.28 |
±1.65 |
| 0.05 |
-1.65 |
+1.65 |
±1.96 |
| 0.01 |
-2.33 |
+2.33 |
±2.58 |
Önem derecesi sosyal bilimlerde genellikle @ = 0.05 veya 0.01 olarak seçilmektedir.
Parametrik Test Varsayımları;
| 1. Örneklemin çekildiği evrenle ilgili |
2. Örneklemle ilgili |
| a- Normal dağılıma sahip olmalı |
a- Denekler evrenden rastgele seçilmeli |
| b- Varyanslar homojen olmalı |
b- Denekler birbirinden bağımsız |
olarak seçilmeli
Bu analizde belirli bir önem derecesinde ana kütle aritmetik ortalamasının belli bir değerden büyük, küçük veya farklı olup olmadığı test edilir.
Örneklem sayısı n>30 ise test istatistiği Z olarak, nó30 ise t istatistiği hesaplanır. Bu istatistiklerin formülleri şöyledir:
|
|
|
Bu test uygulanarak, iddia edilen ana kütle ortalamasının gerçek olup olmadığı ve örneğin bu ana kütleye ait olup olmadığı hakkında da fikir verir.
Bu testin serbestlik derecesi (n-1)'dir.
ÖRNEK: Bir işletmenin yıllık ortalama üretim miktarı düzenli olarak kaydedilmiş ve ortalaması 500 olarak bulunmuştur. Bu yılki üretimi denetlemek isteyen yöneticiler üretimden 100 adet örneklem almış ve ortalamasını X=490, standart sapması S=40 olarak bulmuştur. %1 güven sınırına göre yıllık üretim miktarlarının ortalaması 500 kabul edilebilir mi? Test ediniz.
ÇÖZÜM: H0: µ1=µ2 ; H1: µ1¹µ2 ;n>30 olduğundan Z testi uygulanacaktır.
| |
|
Serbestlik derecesi n-1 =100-1=99 olarak bulunur.
0.01 güven düzeyinde çift yönlü test kritik değeri=2.58
ZHesap< ZTablo; 2.5<2.58 olduğundan H0 kabul, H1 ret edilir.
Sonuç: iki ortalama arasında fark yoktur. (z=2.5, p<.01)
Ana kütlenin herhangi bir niteliğinin belirli bir orandan büyük, küçük veya farklı olup olmadığının test edilmesinde kullanılır.
n>30 ise z istatistiği, n<30 ise t istatistiği hesaplanır.Bu istatistiklerin formulleri şöyledir.
|
|
|
ÖRNEK: Pazar payının %40'ını elinde bulundurduğunu idda eden bir firma satışları ile ilgili yapılan ve 82 birimi kapsayan örneklemde sözkonusu oranı %35 bulmuştur. %5 güven düzeyinde iddanın doğruluğunu tespit ediniz.
ÇÖZÜM: H0 : p - P = 0 ; H1 : p - P ¹ 0 ; p=%35; P=%40; n=82; @=0.05
| |
|
Serbestlik derecesi = n-1 = 82-1=81 olarak bulunur.
0.05 güven düzeyinde çift yönlü test kritik değeri=1.96 dır.
ZHesap< ZTablo; -0.92<1.96 olduğundan H0 kabul H1 ret edilir.
Sonuç: iki oran arasında fark yoktur. (z=-0.92, p<.05) İddia geçerlidir.
6.1.3. İki Örnek Ortalamasının Karşılaştırılması (Bağımsız gruplarda T testi)">
Birbirinden bağımsız iki örneklemin ortalamaları arasındaki farkın hangi yönde olduğu ve bu farkın önemli olup olmadığı test edilmesinde kullanılır.
| Örneklem büyüklüğüne göre n>30 ise z, istatistiği n<30 ise t istatistiği hesaplanır. |
|
|
|
|
|
|
|
Bu testte serbestlik derecesi (n1+n2 -2)'dir.
ÖRNEK SORU: Bir işletmede iki vardiya şeklinde üretim yapılmaktadır. Birinci
grup 40 günlük çalışma sonunda ortalama 74 parça üretimde bulunmuş ve standart sapması 8 olarak hesaplanmıştır. İkinci grup ise 50 günlük çalışma sonunda ortalama 78 parça üreterek 7 standart sapma ile çalışmışlardır. %5 güven sınırlarında iki grubun ortalamaları farklı mıdır?
ÇÖZÜM: n1=40 ; X1=74; S1=8; n2=50; X2=78; S2=7; @=0.05
Hipotezler: H0 =X1-X2=0 ; H1 =X1-X2¹0
| |
|
| |
|
Serbestlik derecesi (n1+n2 -2) = 40+50-2 =88 olarak bulunur.
0.05 güven düzeyinde çift yönlü test kritik değeri=1.96 dır.
ZHesap> ZTablo; 2.49>1.96 olduğundan H0 reddedilir.
Sonuç: iki ortalama arasında fark vardır. (z=-2.49, p<.05)
İki örnek için oranlar hesaplanmış ise; bu oranlar arası fark ve bu farkın önemi test edilir. Serbestlik derecesi (n1+n2 -2) şeklinde hesaplanır.
Hesaplama için n>30 ise z istatistiği, n<30 ise t istatistiği hesaplanır.Bu istatistiklerin formulleri şöyledir:
|
|
|
Bu testte serbestlik derecesi (n1+n2 -2)'dir.
ÖRNEK: Bir şampuan üreticisi, iki farklı şehirde 100'er kişilik gruplar üzerinde bir araştırma yaparak şampuan kullananların oranını belirlemiştir. Birinci şehirde %75; ikinci şehirde ise %65 olumlu yanıt almışlardır. İki şehirdeki kullanıcı oranları arasında fark olup olmadığını 0.05 güven düzeyinde test ediniz.
ÇÖZÜM: P1=0.75; P2=0.65; n1=100; n2=100; @=0.05
Hipotezler: H0 : P1- P2 = 0 ; H1 : P1 - P2 ¹ 0 ;n=100 olduğundan z testi kullanılır.
| |
|
Serbestlik derecesi (n1+n2 -2) = 100+100-2 =198 olarak bulunur.
0.05 güven düzeyinde çift yönlü test kritik değeri=1.96 dır.
ZHesap> ZTablo; 2.22>1.96 olduğundan H0 reddedilir.
Sonuç: iki oran arasında fark yoktur. (z=2.22, p<.05)
İkiden çok örnek kütle ortalamalarının karşılaştırılmasında kullanılır.
Bu yöntemle toplam değişmeye katkıda bulunan çeşitli değişim kaynaklarının değişkenler arası etkileşimi ve deneysel hataları incelenir.
Varyans analizi tek yönlü ve çok yönlü olarak uygulanabilir. Tek yönlü varyans analizi elle hesaplanabilir, ancak çok yönlü varyans analizi için bilgisayar kullanılmalıdır. Bu yöntemle ilgili aşağıdaki hususlara dikkat edilmelidir:
1. Gruplardaki bireyler birbirine benzer ve homojen olmalıdır.
2. Gruplar birbirinden bağımsız olmalıdır. Bağımlı gruba uygulanmaz.
3. Veriler ölçümle belirlenmiş sürekli karakter olmalıdır.
4. Gruplardaki denek sayısı(n) en az 20 olmalıdır.
5. Gruptaki denek sayıları birbirine eşit veya yakın olmalıdır.
Bu şartlar sağlanamadığı zaman nonparametrik karşılığı "Kruskal Wallis varyans analizi" uygulanmalıdır.
ÖRNEK: İşletmede bulunan üç eşdeğer makina üretimi aşağıdaki gibidir. Bu üç makina arasında fark var mıdır?
| A |
B |
C |
Toplam | |
| 4 |
6 |
3 |
||
| 5 |
7 |
4 |
||
| 5 |
6 |
5 |
||
| 4 |
8 |
5 |
||
| 6 |
6 |
4 |
||
| 6 |
7 |
4 |
||
| 4 |
9 |
3 |
||
| 5 |
8 |
3 |
||
| 4 |
6 |
4 |
||
| 4 |
5 |
3 |
||
| Sx | 47 | 68 | 38 | 153 (Sx) |
| Sx2 | 227 | 476 | 150 | 853 (Sx2) |
| nj | 10 | 10 | 10 | 30 (Sn) |
I. Kareler toplamlarının bulunması:
GnKT:Genel Kareler Toplamı
![]()
GAKT: Gruplar arası kareler toplamı
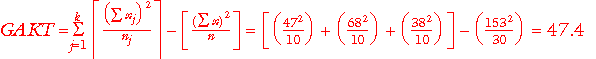
GiKT: Grup içi kareler toplamı
![]()
Serbestlik Derecelerinin Bulunması:
Genel serbestlik derecesi: GnSD= n-1 =30-1=29
Gruplar arası serbestlik derecesi: GASD=Grup sayısı-1=3-1=2
Grup içi serbestlik derecesi: GiSD= n-Grup sayısı=30-3=27
Kareler Ortalamasının Bulunması:
Gruplar arası kareler ortalaması:
![]()
Grup içi kareler ortalaması:
![]()
Varyasyon Kaynağı Tablosunun Hazırlanması:
| Varyasyon Kaynağı | Kareler Toplamı | Serbestlik Derecesi | Kareler Ortalaması |
VK |
KT |
SD |
KO |
| Gn |
72.7 |
29 |
---- |
| GA |
47.4 |
2 |
23.7 |
| Gi |
25.3 |
27 |
0.937 |
Hipotezler: H0: Gruplar arası fark yoktur. H1: Gruplar arasında fark vardır.
Test istatistiği olarak F istatistiği kullanılır.
![]()
Yanılma olasılığı (güven düzeyi)@ =0.05 seçilmiştir.
Varyans analizinde iki serbestlik derecesi kullanılır.
Gruplar arası serbestlik derecesi=2 Grup içi serbestlik derecesi=27
F tablo değeri bulunur. F=3.35
Karşılaştırma: FHesap=25.3 FTablo = 2.35 ; 25.3 > 2.35 olduğundan H0 red edilir.
Sonuç: Gruplar arasında fark vardır. Üç makinenın üretimi arasında anlamlı bir fark bulunmuştur. Bundan sonra gruplar ikişer ikişer karşılaştırılır. Bu karşılaştırmada t testi kullanılır. Bu şekilde karşılaştırılan ortalamalar sıralanır ve önem denetimi yapılır.
Korelasyon analizinde iki veya daha çok sayıda değişken arasında bir ilişki bulunup bulunmadığı, eğer varsa bu ilişkinin derecesi ve fonksiyonel şekli belirlenmeye çalışılır. Örneğin reklamların satışı arttırdığı şeklinde bir düşünce yaygındır. Ancak satışların artışı sadece reklamlar ile açıklanamaz. Nüfus artışı, moda, fiyat rakiplerle rekabet satışları etkileyen diğer nedenler olarak düşünülebilir. Öyle ise reklamlar ile satış arasında ilişkinin olup olmadığı incelenmelidir.
7.1. Doğrusal Korelasyon: Bir değişkenin değeri artarken diğer değişkenin değeri düzenli artıyor veya eksiliyorsa iki değişken arasındaki ilişki doğrusaldır. İlişki grafik üzerinden de incelenebilir.
|
|
|
|
| Korelasyon=+1 |
Korelasyon=-1 |
Korelasyon=0 |
Doğrusal korelasyonun hesaplanmasında Pearson Momentler Çarpımı korelasyonu kullanılır. Bu formülün uygulanabilmesi için veriler en az aralıklı ölçekle toplanmalı ve süreklilik gösteren nicel bir değişken olmalıdır.
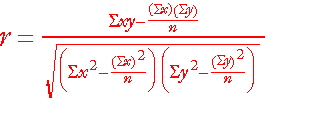
Korelasyon katsayısının değeri -1 ile +1 arasında değişir. Sonucun +1 çıkması iki değişken arasında kuvvetli olumlu ilişkinin bulunduğunu, -1 ise kuvvetli olumsuz ilişkinin bulunduğunu gösterir. Korelasyon katsayısı 0 'a yaklaştıkça ilişkinin kuvveti zayıflar, sıfır ise iki değişken arasında ilişkinin olmadığını gösterir.
7.1. Korelasyon katsayısının önem denetimi:
Hesaplanmış olan korelasyon katsayısının tesadüfi mi yoksa gerçek bir ilişkiyi mi gösterdiğinin belirlenmesi için denetlenmesi gerekir.Denetim için kurulan hipotezler H0 : j=0 ; H1 : j ¹ 0 şeklinde belirlenir. Test istatistiği şu formüle göre hesaplanır,
![]()
r:Korelasyon katsayısını belirtir. Serbestlik derecesi (n-2) dir.
ÖRNEK: Aşağıda bir işletmede gün olarak kullanılan izin (X) ile performans puanları (Y) verilmiştir. Bu iki değişken arasında ilişki var mıdır?
| X |
Y |
X2 |
Y2 |
XY |
| 1 |
14 |
1 |
196 |
14 |
| 2 |
13 |
4 |
169 |
26 |
| 3 |
12 |
9 |
144 |
36 |
| 3 |
13 |
9 |
169 |
39 |
| 2 |
11 |
4 |
121 |
22 |
| 1 |
12 |
1 |
144 |
12 |
| 4 |
12 |
16 |
144 |
48 |
| 5 |
11 |
25 |
121 |
55 |
| 4 |
14 |
16 |
196 |
56 |
| 3 |
13 |
9 |
169 |
39 |
| 6 |
12 |
36 |
144 |
72 |
| 5 |
12 |
25 |
144 |
60 |
| 10 |
10 |
100 |
100 |
100 |
| 9 |
11 |
81 |
121 |
99 |
| 1 |
14 |
1 |
196 |
14 |
| 8 |
11 |
64 |
121 |
88 |
| 9 |
10 |
81 |
100 |
90 |
| 7 |
9 |
49 |
81 |
63 |
| 6 |
12 |
36 |
144 |
72 |
| 7 |
10 |
49 |
100 |
70 |
| Sx 96 | Sy 236 | Sx2 616 | Sy2 2824 | Sxy 1075 |
Yukarıdaki tabloda hesaplanan değerler formülde yerine konduğunda;
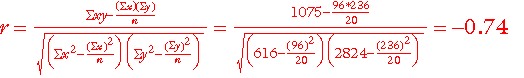
Elde edilen sonuca göre kullanılan izin miktarı ile performans puanları arasında negatif yönlü kuvvetli ilişki vardır. Kullanılan izin miktarı arttıkça performans puanları düşmektedir.
Bulunan korelasyonun gerçekten önemli olup olmadığı incelenirse:
Hipotezler, H0 : j=0 ; H1 : j ¹ 0

Serbestlik derecesi :(n-2)=20-2=18
0.05 güven düzeyinde çift yönlü test kritik değeri=2.1 dır.
ZHesap> ZTablo; 4.8>2.1 olduğundan H0 reddedilir.
Sonuç: Bulunan korelasyon önemlidir ve tesadüfi değildir.(t=4.8, p<.05)
Bu belge İstatistik hakkında temel kavramlar ve bazi örnekleri içermektedir. Kaynak göstermek koşulu ile alıntı yapılabilir.
| © Cahit Cengizhan 2001-2003 Ders Notları Arşivinden |