FORSCHUNGSMETHODEN SKRIPTUM

GRUNDKONZEPTE

Forschung ist die systematische Sammlung, Aufbereitung, Analyse und Interpretation von Daten, welch ist genau der Begriff der Statistik, über die Eigenschaften und Beeinflussungsmöglichkeiten zum Zweck der Informationsgewinnung für akademische und industrielle Entscheidungen.

Forschung ist die Ansammlung und die Analyse von Daten von einer Probe der Einzelpersonen oder der Organisationen, die auf ihrer Eigenschaft, Verhalten, Haltung, Meinungen oder Besitz in Verbindung gestanden werden. Sie schließt alle Formen der Forschung wie Verbraucher- und Industrieerhebung, psychologische Untersuchungen, Beobachtungen und Panelstudien ein. Forschung unterscheidet sich von der bloßen Markterkundung durch den systematischen Einsatz wissenschaftlicher Untersuchungsmethoden. Demgegenüber unterscheiden sich Forschung und Marketing-Forschung durch ihren jeweiligen Untersuchungsgegenstand. Der in den USA weitverbreiteten Begriff der Marketing-Forschung ist gegen oben vorgeschlagener Begriffsdefinition auf Informationsbereitstellungen für Absatzentscheidungen eingeengt. Drei Hauptarbeitsgebieten nach Schäfer (1978) sind nämlich Bedarfsforschung, Konkurrenzforschung und Erforschung der Absatzwege. Dagegen hat nach Behrens (1966) die Forschung zwei Arbeitsgebiete zum Gegenstand:

· die ökoskopische Forschung, die der Erforschung ökonomischer Größen wie Marktanteile, Umsätze, Preise u.a.m. dient;

· die demoskopische Forschung, die sich um die Erforschung der äußeren und inneren d.h. psychischen Merkmale von Marktteilnehmern bemüht.

Beide Einteilungen seht man nicht ausreichend. Statt dessen sollen i folgenden einige wichtige Gliederungsgesichtspunkte herangezogen, die stärker auf die Informationsbereitstellung für Marketing-Entscheidungen abheben;

· die Elemente von Marketing-Entscheidungen,

· die Art des Marketing-Entscheidungsproblems,

· die Phasen des Marketing-Entscheidungsprozesses.

MÖGLICHE FEHLERQUELLEN IN EINER FORSCHUNGSTUDIE

Ob Sie Forschung oder Messwert konzipieren und ihn auswerten, ist es nützlich, sich der Aufgabe als eine von Steuerung für oder von Suchen nach Fehlern zu nähern. Das folgende ist eine Liste der Typen für zu überwachen der Fehler, wenn es Forschung konzipiert oder Forschung Reports liest. Die Grundregeln und die Methoden, die wir behandeln, sind groß konzipiert, um für Fehler zu steuern.

· Problemdarstellung: Konzeptualisierung des Forschung Problems kann nicht die reale Situation ausreichend oder genau reflektieren.

· Gebrauch von einer Theorie oder Annahmen, die fehlerhaft sind oder nicht

· Forschung Problem anwenden, adressiert nicht das Managementfragen

· reductionism - Auslassung von Schlüsselvariablen

· Stellvertretender Informationen Fehler: Variante zwischen den Informationen benötigt, um das Problem und die Informationen zu lösen gesucht vom Forscher.

· Meßfehler: Variante zwischen den gesuchten Informationen und den Informationen produzierte durch den Messen-Prozeß (Zuverlässigkeit und Gültigkeit).

· Grundgesamtheit Spezifikation Fehler: Variante zwischen der Grundgesamtheit benötigt, erforderliche Informationen und die Grundgesamtheit zur Verfügung zu stellen gesucht vom Forscher (Richtlinie für die Studie Grundgesamtheit offenbar definieren).

· Feldfehler: Variante zwischen der Grundgesamtheit, wie durch den Forscher und die Liste der Einheiten einer Grundgesamtheit definiert benutzt vom Forscher.

· Stichprobenfehler: Variante zwischen einer Repräsentativprobe und der Probe festgelegt durch eine Stichprobenauswahlmethode (Stichprobenfehlerschätzungen, überprüfend auf Vorstellung).

· Auswahlfehler: Variante zwischen einer Repräsentativprobe und der Probe erhalten durch ein nonprobability Stichprobenverfahren (Überprüfung auf Vorstellung).

· Nonresponsefehler: Variante zwischen der Probe, die ausgewählt wurde und der, die wirklich an der Studie teilnahm (auswertende Non-responsevorspannung).

· Experimenteller Fehler: Variante zwischen der tatsächlichen Auswirkung der Behandlung und der Auswirkung schrieb ihr gründete auf einem experimentellen Design zu (Vormessen, Interaktion, Auswahl, Geschichte, Entwicklung, Instrumentenausrüstung, Sterblichkeit, reagierender Fehler, Zeitbegrenzung, stellvertretende Situation - definiert später, wenn wir experimentelles Design umfassen). (experimentelles Design)

· Datenverarbeitende Fehler: Fehler in der Kodierung und im Handhaben von Daten (Reinigung).

· Analyse Fehler: Umfaßt eine Vielzahl von Fehlern einschließlich Verletzung von Annahmen der statistischen Prozeduren, des Gebrauches von nicht angebrachten oder falschen Prozeduren, der Mißhandlung der fehlenden Werte, der Berechnung Fehler und der fehlerhaften Deutung von Resultaten.

· Bericht und Kommunikation Fehler: Fehler gemacht, wenn Mund- oder schriftliche Reports einschließlich die typographischen und logischen Fehler vorbereitet werden. Fehlerhafte Deutung der Resultate gebildet von den Benutzern (Bearbeiten).

· Anwendung Fehler: Nicht angebrachte oder fehlerhafte Anwendung der Forschungsresultate zu einem Managementproblem. die Resultate zu den Situationen Über-zu generalisieren, in denen sie möglicherweise nicht zutreffen können, ist ein geläufiger Fehler, wenn sie Forschungsresultate anwendet.

1. Phasen des Forschungsprozesses

Jeder Forschungsprozess und damit auch ein Forschungsprojekt läbt sich als Abfolge von Arbeitsschritten darstellen.

1. Problemformulierung und Wahl des Forschungsdesigns

2. Bestimmung der Informationsquellen und Erhebungsmethoden

3. Operationalisierung und Messung der einbezogenen Variablen

4. Durchführung der Erhebung

5. Vorbereitung der Datenauswertung

6. Datenauswertung und Ergebnisinterpretation

7. Erstellung des Forschungsberichts und Präsentation der Ergebnisse

1.1 Problemformulierung und Wahl des Forschungsdesigns

Der erste Schritt des Forschungsprozesses beinhaltet eine möglichst präzise Beschreibung des Forschungsproblems. Bei geringen Kenntnisstand über das zu lösende Entscheidungsproblem ist ein möglichst flexibler Forschungsprozess sogenannte explorative Forschung in die Wege zu leiten, während bei genauer Kenntnis ein detaillierter Forschungsplan erstellt werden kann, in dem festhalten wird, welche Daten auf welchem Wege zu erheben und auszuwerten sind. Als Forschungsdesigns kommen hierbei die deskriptive oder die experimentelle Forschung in Frage. Die präzise Formulierung des Forschungsproblems wird in der Wissenschaftstheorie unter dem Begriff der Hypothesenformulierung diskutiert (Beispiele werden gegeben). Die kausale und deskriptive Hypothesen lassen sich gewissermaßen als Forschungsziele betrachten, die in die Form einer Behauptung gekleidet sind, wo die Erklärung, Prognose und damit die Unterstützung von Entscheidungen möglich ist. Wenn das Entscheidungsproblem sehr vage bekannt ist, dient die explorative Forschung dem Zweck der Hypothesenfindung.

1.1.1 Explorative Forschung

Im wesentlichen werden mit ihr folgende Forschungsziele angestrebt:

· Präzisierung von Marketing-entscheidungs- und Forschungsproblemen, Hypothesenfindung,

· Prioritätensetzung für die Projektauswahl

· Anhaltspunkte für die Projektabwicklung

Obwohl in dieser vorwissenschaftlichen Erkundungsphase ein hohes Maß an Flexibilität und Kreativität der Forscher erforderlich ist, haben sich einige Erhebungsmethoden für sie bewährt.

1. Literatursichtung und Sekundärforschung: Literaturstudium und die Analyse bereits vorliegender interner und externer Daten sollten stets den ersten Untersuchungsschritt eines Forschungsvorhabens bilden. Hierdurch lassen sich schnell und mit geringen Kosten zusätzliche Einsichten hinsichtlich der Ursachen des Problems, der infrage kommenden Handlungsalternativen und für die weitere Projektgestaltung gewinnen.

2. Expertenbefragung: Wertvolle Anregungen lassen sich durch die Expertenbefragung, unstrukturierte persönliche tiefen Interview, wenn bei bedeutenden Forschungsvorhaben oder relativ neuartigen Problemstellungen die Sichtung vorhandenen Materials nicht genügt.

1.1.2 Deskriptive Forschung

Die Forschungsziele deskriptiver Studien lassen sich in drei Kategorien einteilen. Die sind Beschreibung von Markttatbeständen und Ermittlung der Häufigkeit ihres Auftretens, Ermittlung des Zusammenhangs zwischen Variablen und Prognosen.

Auch die Methoden der Informationsbeschaffung unterscheiden sich von der explorativen Forschung: im Vordergrund steht die standardisierte Befragung bzw. Beobachtung repräsentativer Stichproben. Daneben kommt noch die systematische (statistische) Analyse von Sekundärdaten insbesondere von Paneldaten in Betracht. Querschnittanalysen handelt sich hierbei um Daten, die sich nur auf einen bestimmten Zeitpunkt beziehen. Bei Längsschnittanalysen werden demgegenüber die Daten zu verschiedenen Zeitpunkten wiederholt erhoben.

1.1.3 Experimentelle Forschung

Ein Experiment dient der Überprüfung einer Kausalhypothese, wobei eine oder mehrere unabhängige Variable(n) durch den Experimentator bei gleichzeitiger Kontrolle aller anderen Einflussfaktoren variiert werden, um die Wirkung der unabhängige(n) Variable(n) messen zu können. (Böhler, 1992)

Zufallsprinzipen: Alle Testeinheiten sind nach dem Zufallsprinzip auswählen und auf die Gruppen zu verteilen. Sie sollen unabhängig voneinander ausgewählt werden.

Interne Validität ist gegeben, wenn die rechnerisch festgestellte Differenz der abhängigen Variablen einzig und allein auf den Experimentfaktor zurückzuführen ist. Der Begriff der externen Validität bezieht sich auf die Generalisierbarkeit (Repräsentanz) der Experimentergebnisse.

1.2 Bestimmung der Informationsquellen und Erhebungsmethoden

Zur Beschaffung der Informationen kann man innerbetriebliche oder außerbetriebliche Quellen heranziehen. Sollen die Informationen aus bereits vorhandenem Datenmaterial gewonnen werden, so handelt es sich um Sekundärforschung. Ist dagegen für das anstehende Forschungsproblem eigens neues Datenmaterial zu beschaffen, so liegt eine Primärforschung vor. Die wichtigste Informationsquelle der Primärforschung sind die Endverbraucher, bei denen die Daten entweder durch Befragung oder durch Beobachtung erhoben werden. Zur Klassifizierung der Befragungsmethoden also teilweise zur Fragebogenaufbauwerden üblicherweise die folgenden Kriterien herangezogen.

· Standardisierungsgrad: standardisierte und teil-/nichtstandardisierte Befragung

· Art der Fragestellung: direkte und indirekte Befragung

· Kommunikationsform: mündliche, telefonische, schriftliche, computergestützte Befragung.

Die Beobachtung ist eine Datenerhebungsmethode, die auf die planmäßige Erfassung sinnlich wahrnehmbarer Tatbestände gerichtet ist, wobei der Beobachter sich gegenüber dem Beobachtungsgegenstand rezeptiv verhält. Arten von Variablen maßen gewöhnlich in Übersichten:

1. Demographische und sozioökonomische Eigenschaften

2. Verhalten

3. Haltung, Interessen, Meinungen, Präferenzen, Vorstellungen

a. kognitiv: Glaubens und Wissen

b. affektiv: Gefühle, emotionale Verhaltens

c. absichten der Warte

1.3 Beispiele von Fragenarten

1) einfach füllen Sie das Leerzeichen aus. Eine direkte Zahl oder andere erreichend, verstand leicht Antwort.

Sind Sie wie alt? ___________; In welcher Grafschaft ist Ihr permanenter Wohnsitz? __________; wieviel Geld Sie auf dieser Reise aufwendete? $ __________________.

2) geöffnetes beendet: Führendes Thema vermeiden, um breite Strecke der Antworten in eigenen Wörtern des Themas zu erhalten oder, wenn Sie nicht Arten von Antworten kennen.

Was ist Ihr Primärgrund für den Park heute besichtigen? _______________________________________.

3) teilweise geschlossen beendet. Drucken Sie Hauptwartekategorien beim Verlassen des Raumes für andere aus.

Welches der folgenden Gemeinschaftserholungteildienste verwenden Sie am häufigsten? (Überprüfung eine).

Tennisgerichte / Bereiche der Nachbarschaft / parks/playgrounds / Swimmingpool / Einkaufszentren / anderes (spezifizieren Sie bitte), ___________________

4) Checklisten: Lassen Sie Themen mehrfache Antworten überprüfen. Die vollständigen Kategorien u. gegenseitig Exklusives

Welche von den folgenden Wintererholungaktivitäten haben Sie während des letzten Monat?(check teil)

Eislaufen / Sledding / Snowmobiling / Abfahrtskilauf / Querfeldeinskiing

5) Likert Skalen: Vielseitiges begabte Format für messende Haltung. Kann "übereinstimmen" mit "Wert"" Zufriedenheit ", "Interesse" "Präferenz" und andere Beschreiber ersetzen, die Haltung zu passen, die Sie messen möchten.

Überprüfen Sie bitte den Kasten, der gut Ihre Stufe der Vereinbarung oder des Widerspruchs mit jeder der folgenden Anweisungen über Abfahrtskilauf darstellt:

Stimmt stark zu Stimmt zu Neutrales Stimmt nicht zu Stimmt stark nicht zu

2 1 0 -1 -2

Abfahrtskilauf ist aufregender

Abfahrtskilauf ist gefährlicher

Abfahrtskilauf ist kostspielige

6) Rank-Einrichtung zu: Zum Maß preferences/priorities. Begrenzung auf kurze Listen.

Ordnen Sie die folgenden Zustände in Ihrem Interesse ausgedrückt, wie möglich, reisen Zieleinheiten für eine Sommerferienreise. Plazieren Sie 1 neben dem Zustand, den Sie die meisten mögen besuchen wurden, plazieren Sie 2 außer Ihrer zweiten Wahl und 3 neben Ihrer dritten Wahl.

______ Michigan

______ Wisconsin

______ Minnesota

7) Filter-Frage. Für Eignung oder Wissen vor dem Stellen anderer Fragen rastern. Stellen Sie sicher, daß jede Frage auf alle Themen zutrifft oder verwenden Sie Filter und Zeilensprünge, um Antwortende um Fragen zu verweisen, die nicht anwenden.

Blieben Sie über Nacht auf Ihrer neuesten Reise? Ja / Nein

WENN JA, wieviele Nächte verbrachten Sie weg vom Haus? ______

8) Skala des semantischen Differentials. Messen Sie Vorstellung oder Bild von etwas, das ein Merkmal von polaren Adjektiven verwendet.

Für jede der Eigenschaften druckte unten, kennzeichnen ein X auf der Zeile aus, in der Sie Abfahrtskilauffällen in Bezug auf charakteristischen den glauben. (könnte mit Kreuzlandski wiederholen und snomobiling und Vorstellungen vergleichen) (oder Koks und Pepsi).

aufregendes _____ ______ ______ ______ ______ ______ stumpfes

kostspieliges _____ ______ _____ ______ ______ ______ billiges

sicheres _____ ______ _____ ______ ______ ______ gefährlich

1.4 Operationalisierung und Messung der einbezogenen Variablen

Die operationale Definition von Eigenschaften erfordert:

· eine präzise theoretisch-begriffliche Fassung der interessierenden Eigenschaften,

· die Angabe der in der Realität wahrnehmbaren Merkmale, die die theoretisch-begriffliche formulierten Eigenschaften repräsentieren und der konkreten Maßnahmen, mit deren Hilfe sie zu messen sind.

Unter Messen versteht man den Vorgang der Datenerhebung mittels Beobachtung oder Befragung und die Zuordnung von Symbolen zu den registrierten Merkmalsausprägungen nach bestimmten Regeln. Bei jedem Skalenniveau sind nur ganz bestimmte Transformationen zulässig.

1.4.1 Typen des Messens und Skalenarten

Quantitative Datenerfassung bezieht gewöhnlich mit ein, Informationen (demographisch, attitudinal, abschätzend, auf Tatsachen beruhend, usw..) zu erwerben von den einzelnen Antwortenden. Der InterviewAblaufplan oder -fragebogen ist die häufig eingesetzten Mittel des Erhaltens solcher Informationen oder Daten. Die bekannteste Einteilung der statistischen Skalen nach ihrem Meßniveau stammt von Stevens. Nominal- und Ordinaleskalen werden als nichtmetrische, Intervall- und Verhältnisskalen als metrische Skalen bezeichnet.

1. Nominalskala ist die einfachste Form des Messens. Die Zahlen dienen lediglich der Bezeichnung von qualitativen Klassen. (Häufigkeit Verteilungen, Modus, Kontingenzkoeffizienten, Chi-Quadrattest)

2. Ordinaleskalen bringen die Untersuchungsobjekte hinsichtlich ihrer Merkmalsausprägungen in eine Rangordnung. Die Zahlen bezeichnen Rangplätze, nicht aber die Quantität einer Eigenschaft. So läbt sich über die Differenzen zwischen den Präferenzen in empirischen System und daher auch über die Abstände zwischen den Zahlen keine Aussage machen. Damit dürfen auch nicht die mathematischen Operationen verwenden. (Häufigkeit Verteilungen, Median, Rangkorrelation, Mann-Whitney-U-Test)

3. Bei Intervallskalen sind die Abstände zwischen zwei Punkten berechenbar und ihnen liegt eine standardisierte Meßeinheit zugrunde. Hierzu zählen die Temperaturskalen sowie einige Einstellungsskalen auf die noch einzugehen ist. Bei hypothetischen Konstrukten ist eine derartige Erfassung von Differenzen nicht möglich. An die Stelle des nicht unmittelbar beobachtbaren empirischen Phänomens wird daher ein Modell gesetzt z.B. Ratingskalen stammt von Thurstones “Law of Comparative Judgement”. Im Grunde liegt somit ein Skalenniveau vor, dab zwischen Ordinale- und Intervallskala liegt. Parallel durchgeführte nichtmetrische und metrische Auswertungen von Daten haben jedoch in vielen Fällen keine gravierenden Unterschiede erbracht, so dab für die praktische Arbeit durchaus von der Annahme des Intervallskalenniveaus ausgegangen werden kann.

4. Verhältnisskala besitzt einen eindeutigen Nullpunkt. Auf ihr sind alle mathematische Operationen anwendbar.

Der Unterschied zwischen den nominalen, Ordnungs- und Abstand waagerecht ausgerichteten Variablen ist nicht schwierig zu verstehen. Was schwieriger zu begreifen ist, ist, warum die Stufen des Messens in der Sozialwissenschaft Forschung so wichtig sind. Statistische Masse entwickelten sich für Daten auf der Abstand Stufe erlauben dem Forscher, die raffinierteste und genaueste Einschätzung vom Bestehen, von der Natur, von der Richtung und von der Stärke der Verbindung zwischen zwei oder mehr Variablen zu bilden. Jedoch besteht viel der Sozialwelt aus Variablen, die nicht auf der Abstand Stufe gemessen werden. Folglich muß der Sozialwissenschaftler vorbereitet werden, die weniger raffinierten und diskriminierenden Datenanalysetechniken zu verwenden, die für die Ordnungs- und nominalen waagerecht ausgerichteten Masse angebracht sind.

Das Schlüssellernziel des Forschers, wenn es Wartekategorien zur Verfügung stellt, ist-, Variablen am ihrem meisten "produktiven" waagerecht ausgerichteten zu messen, damit die leistungsfähigeren statistischen Techniken angebracht sind. Jedoch ist es auch wichtig, daß die Wartekategorien verständlich und zum Antwortenden aussagefähig sind-, aus Furcht daß fehlerhafte Informationen eingeholt werden.

1.4.2 Typen Der Haltungsskalen

Es gibt im Wesentlichen 3 Typen Skalen -- differentiale Skalen, summated Skalen und kumulative Skalen. Im folgenden Kapitel behandeln wir die eindeutigen Merkmale jedes Typen Skala und zu behandeln gut bekannt tippt zeitgenössischen soziologischen Gebrauch ein.

1.4.2.1 Differentiale Skala

Eine differentiale Skala benötigt, daß die Antwort eines Themas spezifiziert, wohin er oder sie entlang irgendein attitudinales Maß fallen. Die besten bekannten Beispiele der differentialen Skalen sind die, die von L. L. Thurstone (Thurstone, 1929) erstellt werden. Thurstone Skalen werden in mehreren Ablaufprozeß hergestellt. Zuerst wird eine offene Frage zu vielen Leuten aufgeworfen. Jede der Antworten zur Frage werden gespeichert und dann zugewiesene Werte durch ein Panel "der sachverständigen" Richter -- basieren auf der Stärke der Haltung, die in der Anweisung ausgedrückt wird. Die Richter weisen unabhängig diese Werte durch das Ablesen und Rank zu, die mehrere unterschiedliche Antworten bestellen, die zur Frage gegeben werden. Gewöhnlich werden die Antworten auf Karten geschrieben und dann sortiert unabhängig von jedem Richter in 10 numerierte Stapel.

In der Praxis wird der differentialen Skalamethode, die von Thurstone erstellt wird, nicht viel heute verwendet. Der Grund für dieses ist, daß Thurstone Skalierung eine extrem zeitraubende Annäherung ist, zum des Aufbaus einzustufen. Ein anderes Problem mit Thurstone Skalen ist, daß sie schnell überholt werden, wenn es Änderungen in der Gesellschaft gibt, welche die Haltung beeinflußt, die gemessen wird. Vor z.B. kann die Anweisung ", das ich glaube, daß ein Mann seiner Frau mit ihrer Arbeit innerhalb des Hauses helfen sollte, ", einer kurzen Zeit wahrgenommen als das Mittelstellung für irgendein Maß von Haltung haben in Richtung zu den gleichmacherischen Geschlechtrollen. Jedoch gleichmäßig mit diesen Problemen, Thurstone Skalen kann im Aufbau der neuen Skalen effektiv verwendet werden.

1.4.2.2 Summende Skalen

Der zweite grundlegende Typ der Skala ist summende Skala. Hier werden die numerischen Werte, die den Wartekategorien für jede Frage zugewiesen werden, einfach hinzugefügt, um eine einzelne Skalakerbe zu produzieren. Summende Skalaannäherung theoretisch Arbeiten, weil Personen, die in Richtung zu irgendeiner Idee sehr stark vorteilhaft sind, häufig auserwählte positive Wartekategorien willen, während die-, die Nullideen haben, irgendein Positiv und einige negative Kategorien auswählen. Schließlich wird es angenommen, daß jene Personen, die dem Konzept entgegengesetzt werden, das gemessen wird, reagieren, indem sie jene Anweisungen auswählen, die eine negative Position reflektieren.

Das geläufigste Formular von summated Skala ist die Likert Skala, entwickelt von Rensis Likert 1932. Gewöhnlich werden eine Anzahl von Anweisungen entwickelt, die gedacht werden, um positive und negative Haltung in Richtung zu irgendeinem Konzept (d.h. Konservatismus, Feminismus, fromme Konventionalität, Vorurteil, usw..) zu reflektieren. Jede Frage wird dann mit einer Anzahl von Wartekategorien geschrieben. Der geläufigste Typ ist die 5 Punkt Likert Skala -- (1) stimmen stark zu, (2) stimmen zu, (3) neutral, (4) anderer Meinung, und (5)stimmen nicht stark zu. Die Kerbe einer Einzelperson würde berechnet, indem man die Werte hinzufügte, die jeder der Antworten zugewiesen werden, die für alle Einzelteile der Skala ausgewählt werden.

1.4.2.3 Kumulative Skala

Der dritte Typ der Skala ist die kumulative Skala. Kumulative Skalen (wie die vorhergehenden zwei Skalen) versuchen, Einzelpersonen entlang irgendeinem Haltung.

Kontinuum in Position zu bringen, indem sie ihnen einzelne Skalakerben zuweisen.

1. Ältere Personen sind normalerweise in ihren Arbeit Fähigkeiten überholt.

____ stimmen zu daß (0 Punkte) das ____SIND anderer Meinung (1 Punkt)

2. Ältere Leute sind normalerweise produktive Arbeiter.

____ stimmen zu daß (1 Punkte) das ____SIND anderer Meinung (0 Punkt)

3. Ältere Arbeiter holen Fähigkeiten und Sachkenntnis zu den Jobs, die jüngere Bauteile nicht zur Verfügung stellen.

____ stimmen zu daß (1 Punkte) das ____SIND anderer Meinung (0 Punkt)

Die Antwortenden, die 1 Punkt zählen, würden mit Frage eine einverstanden SEIN; die Antwortenden, die 2 Punkte zählen, würden mit Frage eine anderer Meinungs SEIN und einverstanden SEIN mit Frage 2; die schließlich Antwortenden, die 3 Punkte zählen, würden mit Fragen 2 einverstanden SEIN und 3 aber anderer Meinungs SEIN mit Frage 1. Mehr Einzelteile auf der Skala, mehr die Abweichung in den Kerben erhalten.

In den vierziger Jahren Louis Guttman (1944) in war sich Entwickeln scalogram Analyse instrumentell. Der resultierende Guttman Koeffizient von Reproduzierbarkeit, ist die statistische Einschätzung des kumulativen Totaleffektes einer Skala. Diese Statistik aktiviert den Forscher, das Eindimensionalität einer Skala zu prüfen.

1.4.3 Skala-Aufbau

Eine Variable einfach garantieren aufzufassen und empirische Anzeigen dann herzustellen, nicht notwendigerweise daß die Variable des Interesses erfolgreich operationalized gewesen ist. In den meisten Forschung Untersuchungen sehen Soziologien die Kreation einer Ansammlung Einzelteile als exakteres Messen eines Konzeptes an. Einfach werden einige Masse oder Einzelteile kombiniert, um in einer einzelnen Skalakerbe anzukommen.

Die Reliabilität spricht die Übereinstimmung eines Masses an. Das heißt, ob sie die gleiche Sache, in der gleichen Methode, oft mißt. Zuverlässigkeit kann für das Erreichen der gleichen Resultate gehalten werden, nachdem man als einmal der gleichen Gruppe der Leute die Übersicht (oder die empirischen Anzeigen) mehr gegeben hat.

· Durch Test-Retest-Verfahren erhält man die Korrelation zwischen den ersten und den zweiten Befragungsergebnissen, die höher ist desto reliable sind die Daten. (Cronbach’s alpha)

· Bei der Split-Half-Technik wird davon ausgegangen, dab das zu messende Konstrukt durch ein Universum beobachtbarer Merkmale repräsentiert wird. Zur Überprüfung der Reliabilität werden die Items (alle möglichen Stimuli) in zwei Hälften geteilt und die Reaktionen der Auskunftspersonen auf beide Itembatterien erfasst.

Die Validität (Gültigkeit) einer Messung ist gegeben, wenn mit dem Mebinstrument genau das gemessen wurde, was der Forscher zu messen beansprucht. Gültigkeit spricht an, ob oder nicht die Fragen oder die empirischen Anzeigen wirklich messen, was sie der Anspruch sind, zum zu messen. Statistisch sprechend, kann Gültigkeit nicht festgestellt werden.

Eindimensionalität spricht die Eigenschaft an, der die Einzelteile, die eine Skala enthalten, ein und nur ein Maß oder Konzept auf einmal messen. Gewöhnlich sind ziemlich komplizierte Konzepte wie fromme Verpflichtung, Feminismus, Vorurteil, Todesangst, eheliche Zufriedenheit und ein Hauptrechner anderer Konzepte mit Skalen und nicht durch einzelne Fragen oder empirische Anzeigen gemessen worden. (Cronbach’s alpha)

Eine andere Ausgabe, die im Aufbau und im Gebrauch der Skalen betrachtet werden muß, ist Reproduzierbarkeit. Die besten Skalen sind die, die Kerbe einer Einzelperson gegeben, wir überzeugt fühlen können, daß er oder sie diese Kerbe resultierend aus einer bestimmten attitudinalen Position erhielten. Cevaplayıcı bütün sorulara aynı yönde cevap vermeli.

1.5 Auswahl der Erhebungseinheiten und Durchführung der Primärerhebung

Sollen Aussagen über eine größere Gesamtheit gemacht werden, eine Möglichkeit ist, die Daten bei allen Einheiten der Grundgesamtheit zu erheben. Diese Vollerhebung (Zensus) kommt in der Marktforschung nur in Frage, wenn die interessierende Gesamtheit relativ klein ist. Meist wird man sich auf eine bestimmte Auswahl aus der Grundgesamtheitsbeschränken, d.h. eine Teilerhebung vornehmen, und von den dort vorgefundenen Ergebnissen auf die Situation in der Gesamtheit schließen, denn Teilerhebungen bieten gegenüber Vollerhebungen mehrere Vorteile:

· Kostenersparnisse,

· weniger Zeitaufwendung,

· Sie sind genauer, d.h. sie enthält weniger systematischer Fehler,

· braucht man weniger Personen,

· weniger Zerstörung der Erhebungseinheiten oder Testeffekt.

Der Auswahlplan umfasst folgende Schritte:

3. Bestimmung der Grundgesamtheit: Sie soll genau definiert und abgrenzt,

4. Bestimmung der Auswahlbasis: Sie ist eine Abbildung der Grundgesamtheit z.B. ein Telefonbuch,

5. Festlegung des Stichprobenumfangs: Nun ist festzulegen, wie viele Erhebungseinheiten in die Auswahl gelangen sollen,

6. Entscheidungen über Auswahlprinzip, -verfahren und -technik,

7. Durchführung der Auswahl.

1.5.1 Auswahlverfahren

Die nicht auf dem Zufallsprinzip beruhende Auswahlverfahren überlassen die Auswahl der Erhebungseinheiten mehr oder weniger dem subjektiven Ermessen des Forschers oder des Interviewers, ohne dab also ein Zufallsmechanismus zum Zuge kommt. Diese Verfahren sind

1. Willkürliche Auswahl: Bei der willkürlichen Auswahl werden die Erhebungseinheiten aus der Grundgesamtheit gewählt, die besonders leicht und bequem zu erreichen sind. Sie ist akzeptabler in der explorativen Phase von Forschungsvorhaben.

2. Konzentrations-/Abschneideverfahren: Wobei werden bestimmte Teile der Grundgesamtheit von der Erhebung ausgeklammert.

3. Typische Auswahl: Sie liegt vor, wenn Erhebungseinheiten herangezogen werden, von denen man annimmt, dab sie am ehesten repräsentativ für die Grundgesamtheit sind.

4. Quotenauswahl: Bei ihr wird die Teilauswahl analog zu der Verteilung einiger Merkmale der Grundgesamtheit aufgebaut. In der Praxis ist man jedoch auf die Merkmale beschränkt, bei denen aus der amtlichen Statistik und sonstigen Veröffentlichungen die Merkmalsverteilung in der Grundgesamtheit bekannt ist. Allerdings zeigen Ergebnisvergleiche zwischen Quotenverfahren und Zufallsverfahren, bei denen ein- und derselbe Fragebogen vorgelegt wurde, bei fast allen Einzelfragen keine nennenswerten Unterschiede. Aus diesem Grunde und wegen der leichten und billigen Abwicklung ist das Quotenverfahren in der Marktforschungspraxis am weitesten verbreitet.

Bei den auf dem Zufallsprinzip beruhende Auswahlverfahren werden die Erhebungseinheiten nicht nach subjektivem Ermessen, sondern durch einen Zufallsmechanismus bestimmt. Somit hat jede Erhebungseinheit eine berechenbare und von Null verschiedene Wahrscheinlichkeit, in die Stichprobe zu gelangen. Hierdurch kommt ein wahrscheinlichkeitstheoretisches Modell zur Geltung, das es ermöglicht, die wahren Werte der Grundgesamtheit (Parameter) anhand der Stichprobenwerte innerhalb bestimmter Bereiche zu schätzen. Die Größe dieser Bereiche hängt von der Streuung des interessierenden Merkmals ab.

	Parameter	Schätzwert
Mittelwert	m	`x
Varianz	s^2	s^2
Anteilswert	p	p
Umfang	N	n
Korrelation	r	r

5. Einfache Zufallsauswahl: Sie läßt sich am besten durch das sogenannte Urnenmodell beschreiben. Jedes Element der Grundgesamtheit nicht nur eine bekannte und von Null verschiedene Wahrscheinlichkeit, sondern darüber hinaus die gleiche Wahrscheinlichkeit (1/N), in die Stichprobe zu gelangen. Beim Stichprobenverfahren wenden wir uns der Verteilungsform der Stichprobenschätzwerte zu. Der zentrale Grenzwertsatz zeigt, dab die Verteilung der statistischen Schätzung mit wachsendem Umfang n gegen eine Normalverteilung strebt.

6. Geschichtete Auswahl: Ziel ist es, die Varianz s² und damit auch den Standardfehler s_`x zu verringern, ohne den Stichprobenumfang erhöhen zu müssen. Zu diesem Zweck wird die Grundgesamtheit in mehrere, sich gegenseitig ausschließende Untergruppen aufgeteilt und aus jeder Untergruppe eine eigene Stichprobe gezogen.

7. Klumpenauswahl: Bei der Klumpenauswahl (cluster sampling) wird die Grundgesamtheit in sich gegenseitig ausschließende Gruppen von Erhebungseinheiten eingeteilt und dann Per Zufallsauswahl eine Anzahl von Klumpen gezogen.

1.5.2 Bestimmung des notwendigen Stichprobenumfangs für Zufallsverfahren

Der Standardfehler beliebig verringert werden kann, wenn man den Stichprobenumfang erhöht. Damit wird auch der Vertrauensbereich enger und die Schätzung der Parameter präziser. Damit verlaufen Sicherheitsgrad und Stichprobenfehler konträr. Der notwendige Umfang kann man bei einem gegebenen Sicherheitsgrad (1-a) und einem maximal zulässigen Konfidenzintervall (e) berechnet.

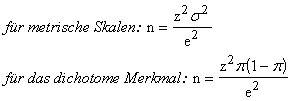
Die Varianz kann man durch Faustregel einschätzen wie s=Wertebereich/6=(X_max-X_min)/6.

2. Datenanalyse

Das Word “Statistik” wurde im 17.Jahrhundert geprägt und bedeutete lange Zeit, die verbale oder numerische Beschreibung der Staatsmerkwürdigkeiten eines Landes und Volkes. Man versteht heute unter dem Word “Statistik” quantitative Informationen über bestimmte Tatbestände wie z.B. “Bevölkerungsstatistik” und zum anderen eine formale Wissenschaft, die sich mit den Methoden der Erhebung, Aufbereitung und Analyse numerischer Daten beschäftigt.

Statistische Methoden benutzt man um eine oder mehrere Merkmale einer Grundgesamtheit (statistische Massen, anakütle) durch die Stichprobenergebnisse (örnek istatistikleri) mit einer bestimmten Wahrscheinlichkeit zu schätzen. Die Elemente der Stichprobe (Teilgesamtheit, örnek) werden Zweckmassigerweise nach gewissen Zufallsprinzipien aus den Grundgesamtheiten ausgewählt.

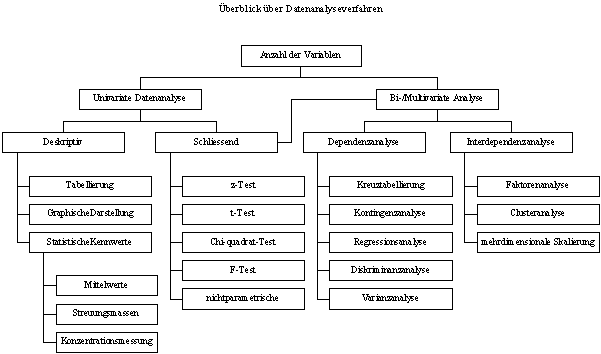
Datenanalyseverfahren lassen sich nach verschiedenen Kriterien klassifizieren. Am gebräuchlichsten sind Einteilungen nach

· Variabelenzahl: uni-, bi- und multivariater Datenanalyse;

· Zielsetzung der Analyse: deskriptive Statistik für die Beschreibung, schließende oder Inferenzstatistik zur Überprüfung der Hypothesen;

· Skalenniveau der Variablen: meist parametrische Techniken anwendet zur Auswertung für metrische Variablen und nichtparametrische für Ordinale;

· Unterteilung der Datenmatrix: bei Unterteilung in zwei Variabelengruppen als Kriteriumsvariablen und Prädiktorvariablen spricht man von der Analyse von Abhängigkeiten (Dependenzanalyse) und wenn nicht unterteilt, dann Interdependenzanalyse.

2.1 Vorbereitung der Datenauswertung

Nachdem in schriftlichen oder persönlichen Interviews die Daten erhoben wurden, sind die ausgefüllten Fragebogen formal und technisch aufzubereiten, damit sie mit Hilfe statistischer Verfahren analysiert werden können. Diese Prozeß besteht aus folgenden Schritten: Aussonderung nicht auswertbarer Fragebogen, redigieren der verwendbaren Fragebogen, Verschlüsselung der Daten (kodieren), Eingabe und Überprüfung der Daten, Hinzufügung neuer Variablen, Gewichtung und Speicherung der Datenmatrix.

Unter Kodieren wird die Bildung von Antwortkategorien und die Zuweisung von Symbolen zu den Antwortkategorien verstanden.

Skala:	Dichotom	Nominal	Ordinale	Klassifizierte Serie	Intervall, Verhältnis
Kodierung:	0, 1	1,2,3,...	..,-2,-1,0,1,2,.. 0,1,2,3,..... 1,2,3,4,.....	Mittelwert der Klasse	erhobene Wert

Nach diesen Aufbereitungsprozeduren liegt eine nxm Datenmatrix vor, die der statistischen Auswertung zugrunde gelegt wird. Da soll man die Kodierung in Tabellen darstellen.

Datenmatrix

Verschlüsslungstabelle

Die Datenbankstruktur ist die Weise, in der Sie beabsichtigen, die Daten für die Studie zu speichern, damit sie in den folgenden Datenanalysen erreicht werden kann. Sie konnten die gleiche Struktur benutzen, die Sie für das Protokollieren in den Daten benutzten, oder, in den großen komplizierten Studien, konnten Sie eine Struktur für Journaldaten und andere für die Speicherung sie haben. Wie oben erwähnt, gibt es im Allgemeinen zwei Optionen für die Speicherung von von Daten auf Computer. Normalerweise sind Datenbankprogramme der zwei das kompliziertere, zum zu erlernen und zu funktionieren, aber sie gestehen dem Analytiker grössere Flexibilität zu, wenn sie die Daten manipulieren. In jedem Forschung Projekt sollten Sie ein gedrucktes codebook festlegen, das die Daten beschreibt und wo anzeigt und wie es erreicht werden kann. Minimal sollte das codebook die folgenden Einzelteile für variables jedes einschließen:

1. variabler Name

2. variable Beschreibung

3. variables Format (Zahl, Daten, Text)

4. instrument/method der Ansammlung. Datum sammelte

5. Antwortender oder Gruppe. variabler Standort (in der Datenbank)

6. Anmerkungen

Das codebook ist ein unentbehrliches Hilfsmittel für das Analyse Team. Zusammen mit der Datenbank sollte es komplette Unterlagen zur Verfügung stellen, die andere Forscher aktiviert, die die Daten analysieren nachher wünschen konnten, um ohne irgendwelche zusätzlichen Informationen so zu tun.

2.1.1 Daten-Transformationen

Sobald die Daten eingegeben worden sind, ist es fast immer notwendig, die rohen Daten in Variablen umzuwandeln, die in den Analysen verwendbar sind. Es gibt eine breite Vielzahl der Transformationen, die Sie durchführen konnten. Einiges vom geläufigeren sind:

2.1.2 Fehlende Werte

Viele Analyse Programme behandeln automatisch unbelegte Werte als Vermißte. In anderen müssen Sie spezifische Werte kennzeichnen, um fehlende Werte darzustellen. Zum Beispiel konnten Sie einen Wert von -99 verwenden, um anzuzeigen, daß das Einzelteil fehlt. Sie müssen das spezifische Programm überprüfen, das Sie pflegen, festzustellen, wie man fehlende Werte bearbeitet.

2.1.3 Einzelteilumlenkungen

Auf Skalen und Übersichten benutzen wir manchmal Umlenkung Einzelteile, um zu helfen, die Möglichkeit eines Wartesets zu verringern. Wenn Sie die Daten analysieren, wünschen Sie alle Kerben, damit Skalaeinzelteile in der gleichen Richtung sind, in der hohe Kerben bedeuten, daß die gleiche Sache und niedrigen Kerben die gleiche Sache bedeuten. In diesen Fällen müssen Sie die Bewertungen für einige der Skalaeinzelteile aufheben. Zum Beispiel lassen Sie uns Sie sagen hatte eine Skala mit fünf Punkten Warte für ein Selbstachtungsmaß, in dem 1 bedeutet stark anderer Meinung und 5 bedeutet stark zustimmen. Ein Einzelteil ist "ich fühlen im Allgemeinen gut über mich." Wenn der Antwortende stark mit diesem Einzelteil einverstanden ist, das sie 5 setzen und dieser Wert würde von der höheren Selbstachtung hinweisend sein. Wechselweise betrachten Sie ein Einzelteil wie "manchmal ich glauben, wie ich bin nicht wert viel als Person." Hier wenn ein Antwortender stark zustimmt, indem er dieses 5 bewertet, würde es niedrige Selbstachtung anzeigen. Um diese zwei Einzelteile zu vergleichen, würden wir die Kerben von einer von ihnen aufheben (vermutlich würden wir das letzte Einzelteil aufheben damit hohe Werte immer höhere Selbstachtung anzeigen). Wir wünschen eine Transformation, in der, wenn der ursprüngliche Wert 1 war, es bis 5 geändert wird, 2 werden geändert bis 4, dieselben des Remains 3, wird 4 bis 2 geändert und 5 wird bis 1 geändert. Während Sie diese Änderungen als unterschiedliche Anweisungen programmieren konnten im meisten Programm, ist es einfacher, dies mit einer einfachen Formel wie zu tun:

Neuer Wert = (Hoher Wert + 1) - Ursprünglicher Wert

In unserem Beispiel ist der hohe Wert für die Skala 5, also, den neuen (umgewandelten) Skalenwert zu erhalten, subtrahieren wir einfach jeden ursprünglichen Wert von 6 (d.h., 5 + 1).

2.1.4 Skalagesamtmengen

Sobald Sie alle einzelnen Skalaeinzelteile umgewandelt haben, wünschen Sie häufig über einzelnen Einzelteilen hinzufügen oder Durchschnitt berechnen, um eine Gesamtkerbe für die Skala zu erhalten.

2.1.5 Kategorien

Für viele Variablen wünschen Sie sie in Kategorien einstürzen. Zum Beispiel können Sie Einkommenschätzungen (in den Dollarmengen) in Einkommenstrecken einstürzen wünschen.

2.1.6 Mögliche Aufgaben der Variablen

Die Variablen dürfen einige Aufgaben bei einem Verfahren erfüllen. Diese Eigenschaft hängt nicht von den Skalatypen von Variablen ab.

· Test Variable: auf die man der Hauptinteresse hat.

• Gruppende Variable: für zwei unabhängige Stichproben.
• Faktor: für Varianzanalyse, mehrere unabhängige Unterteilgesamtheiten.
• Kovariate: die Variable, deren Einfluss auf einen anderen Variable bekannt ist.
• Abhängige Variable: die Variable/-n, auf denen anderen Variablen einen Effekt haben können.
• Unabhängige Variable /-n: die Variablen, die einen anderen Variable einflüssen können.
• Schlumpfvariable: eine Variable, die nur als 0 und 1 kodierte zwei Ausprägungen hat
• Item (Einzelteil einer Haltungsskala): die Variablen, die Messindikatoren einer Variable (zB. Soziale Eigenschaften: Gastfreundschaft) sind.

2.2 Descriptive Statistik

Beschreibende Statistiken werden verwendet, um die grundlegenden Merkmale der Daten in einer Studie zu beschreiben. Sie liefern einfache Zusammenfassungen über die Probe und die Masse. Zusammen mit einfacher Graphikanalyse bilden sie die Grundlage praktisch jeder quantitativen Analyse von Daten.

Beschreibende Statistiken sind von den induktiven Statistik gewöhnlich bemerkenswert. Mit beschreibenden Statistiken beschreiben Sie einfach, was ist, oder was die Daten zeigen. Mit gefolgerten Statistiken versuchen Sie, Zusammenfassungen zu erreichen, die über den Direktdaten hinaus alleine sich ausdehnen. Zum Beispiel verwenden wir gefolgerte Statistiken, um zu versuchen, von den Beispieldaten zu schließen, was die Bevölkerung denken konnte. Oder, wir verwenden gefolgerte Statistiken, um Urteile von der Wahrscheinlichkeit zu bilden, daß ein beobachteter Unterschied zwischen Gruppen ein zuverlässiges oder eins ist, die zufällig in dieser Studie geschehen sein konnten. So verwenden wir gefolgerte Statistiken, um Folgerungen von unseren Daten zu den allgemeineren Bedingungen zu bilden; wir verwenden beschreibende Statistiken einfach, um zu beschreiben, was an in unsere Daten geht.

Beschreibende Statistiken werden verwendet, um quantitative Beschreibungen in einer handlichen Form darzustellen. In einer Forschung Studie können wir Lots Masse haben. Oder wir können viele Leute auf irgendeinem Maß messen. Beschreibende Statistiken helfen uns zu den einfach großen Mengen Daten in einer vernünftigen Methode. Jede beschreibende Statistik verringert Lots Daten in eine einfachere Zusammenfassung. Zum Beispiel betrachten Sie eine einfache Zahl verwendet, um zusammenzufassen, wie gut einer Schläger im Baseball durchführt, der Schlagendurchschnitt. Diese einzelne Zahl ist einfach die Zahl den Hits, die durch die Zahl Zeiten am Hieb geteilt werden (berichtet drei bedeutende Digits). Einer Schläger, der 333 schlägt, erhält einen Hit einmal in jeden drei an den Hieben. Einer Schläger 0.250 schlägt einmal in vier. Die einzelne Zahl beschreibt viele getrennte Fälle. Oder, betrachten Sie den Scourge vieler Kursteilnehmer, den Grad-Punkt-Durchschnitt (GPA). Diese einzelne Zahl beschreibt die allgemeine Leistung eines Kursteilnehmers über eine möglicherweise breite Strecke selbstverständlich Erfahrungen.

Jedes Mal wenn Sie versuchen, ein großes Set Beobachtungen mit einer einzelnen Anzeige zu beschreiben, lassen Sie die Gefahr des Verzerrens der ursprünglichen Daten laufen, oder Schlusse wichtige schildern genau. Der Schlagendurchschnitt erklärt Ihnen, ob nicht der Schläger Ausgangsdurchläufe schlägt oder singles. Er erklärt nicht, ob sie in einem Absacken oder auf einem Streifen gewesen wird. Das GPA erklärt Ihnen, ob der Kursteilnehmer in den schwierigen Kursen oder den einfachen in war oder ob nicht sie Kurse auf ihrem Hauptgebiet oder in anderen Disziplinen waren. Diese Beschränkungen sogar gegeben, liefern beschreibende Statistiken eine leistungsfähige Zusammenfassung, die Vergleiche über Leuten oder anderen Maßeinheiten aktivieren kann.

2.2.1 Univariate Analyse

Univariate Analyse hat die wichtige Arbeitsschritte, die sind tabellarische und graphische Darstellung der absoluten oder/und relativen Häufigkeitsverteilung eines Merkmals, Berechnung von Maßen der zentralen Tendenz (Lageparameter), Ermittlung von Streuungsmaßen zur Kennzeichnung der Homogenität der Untersuchungseinheiten in Bezug auf das untersuchte Merkmal, Messungen von Symmetrie (skewness) und Kurtossis zur Bestimmung der Verteilung. (N: wenn sie normalverteilt, K: nur in klassifizierten Daten)

	Skala
Kollektivmaß	Nominal	Ordinale	Intervall	Verhältnis
Häufigkeitspolygon, Histogramm	X	X	K	K
Modus	X	X	X	X
Median		X	X	X
Arithmetisches Mittel		N	X	X
Quadratisches Mittel		N	X	X
Geometrisches Mittel				X
Spannweite		X	X	X
Mittlere absolute Abweichung			X	X
Varianz, Standardabweichung		N	X	X
Variationskoeffizient				X
Pearson’s Symmetrie		N	X	X
Moment Symmetrie			X	X
Moment Kurtossis			X	X
Lorenz’ Koeffizient			X	X

In der Tabelle, sei zum Anschlub eine Übersicht darüber gegeben, welches Skalenniveau erreicht sein mub, damit man einen bestimmten Mittelwert oder ein bestimmten Streuungsmab sinnvoll berechnen kann.

2.2.2 Empirische Verteilungen

Die Verteilung ist eine Zusammenfassung der Frequenz der einzelnen Werte oder der Strecken der Werte für eine Variable. Die einfachste Verteilung würde jeden Wert einer Variable und der Zahl Personen ausdrucken, die jeden Wert hatten. Zum Beispiel ist eine typische Methode, die Verteilung der Studenten zu beschreiben bis zum Jahr in der Hochschule und druckt die Zahl oder die Prozente Kursteilnehmern an jedem der vier Jahre aus. Oder, wir beschreiben Geschlecht, indem wir die Zahl oder die Prozente Männern und Frauen ausdrucken. In diesen Fällen hat die Variable wenige genügende Werte, daß wir jedes ausdrucken und zusammenfassen können, wieviele Beispielkästen den Wert hatten. Aber was tun wir für eine Variable wie Einkommen oder GPA? Mit diesen Variablen kann es viele mögliche Werte geben, wenn verhältnismäßig wenige Leute jedes haben. In diesem Fall gruppieren wir die rohen Kerben in Kategorien entsprechend Strecken der Werte. Zum Beispiel konnten wir GPA betrachten entsprechend den Zeichengradstrecken. Oder, wir konnten Einkommen in vier oder fünf Strecken der Einkommenwerte gruppieren.

Tabelle 1. Häufigkeitsverteilungskurve Tabelle.

Eine der geläufigsten Methoden, eine einzelne Variable zu beschreiben ist mit einer Häufigkeitsverteilungskurve. Abhängig von der bestimmten Variable können alle Datenwerte dargestellt werden, oder Sie können die Werte in Kategorien zuerst gruppieren (z.B., mit Alter, Preis oder Temperaturvariablen, würde er normalerweise nicht vernünftig sein, die Frequenzen für jeden Wert festzustellen. Eher werden der Wert in Strecken und in die festgestellten Frequenzen gruppiert). Häufigkeitsverteilungskurven können in zwei Möglichkeiten, als Tabelle oder als Diagramm bildlich dargestellt werden. Tabelle 1 zeigt eine Alter Häufigkeitsverteilungskurve mit fünf Kategorien definierte Alter Strecken. Die gleiche Häufigkeitsverteilungskurve kann in einem Diagramm bildlich dargestellt werden, wie in Abbildung 2 gezeigt worden. Dieser Typ des Diagramms gekennzeichnet häufig als ein Histogramm oder ein Balkendiagramm.

Tabelle 2. Häufigkeitsverteilungskurve Balkendiagramm.

Verteilungen können mit Prozentsätzen auch angezeigt werden. Z.B. konnten Sie Prozentsätze verwenden, um zu beschreiben:

7. Prozentsatz der Leute in den unterschiedlichen Einkommensniveaus

8. Prozentsatz der Leute in den unterschiedlichen Alter Strecken

9. Prozentsatz der Leute in den unterschiedlichen Strecken der standardisierten Testkerben

Bei einer statistische Gesamtheit mit n Elementen beobachtet man ein einziges Merkmal (X), das hat k Merkmalausprägungen X_i:X₁, X₂, ...., X_k. So ist f_i, “die absolute Häufigkeit” (frekans) die Anzahl der Elemente, welche die Merkmalausprägung X_i besitzen. Dann erhält man “die relativen Häufigkeiten” (oransal frekans/ olasılık) p_i=f_i/n, wo 0£f_i£n, 0£p_i£1. Die Darstellung der Merkmalsausprägungen X_i mit den dazu gehörenden Häufigkeiten f_i bzw p_i in tabellarischer oder graphischer Form bezeihnet man als Häufigkeitsverteilung (sıklık/frekans dağılımı).

Beispiel#1: Die Examensnoten aus einer Klasse sind als eine “Urliste” darunter gegeben. Damit kann man eine Strichliste aufbereitet. Dieses Merkmal besitzt diskrete Ausprägungen.

5	4	3	3	6	7	6	9	3	4	2	6	5	5	7	6	5	7	5	6
3	4	5	8	2	7	9	8	4	4	5	6	8	5	6	5	3	5	7	4

Häufigkeitsverteilung

Nr. i	Examensnoten Xi	Anzahl der Noten fi	Anteil in der Klasse pi	Prozentanteil 100pi	Summenhäufig.
1	2	2	0.05	5.0	2
2	3	5	0.125	12.5	7
3	4	6	0.15	15.0	13
4	5	10	0.25	25.0	23
5	6	7	0.175	17.5	30
6	7	5	0.125	12.5	35
7	8	3	0.075	7.5	38
8	9	2	0.05	5.0	40
	Summe S	40	1.000	100

Häufigkeiten werden durch Stabdiagramm (Strecken), durch Histogramm (Flächen) oder durch das Häufigkeitspolygon beschrieben. Also durch die absolute/ relative Summenhäufigkeiten antwortet man die Frage ob wie viele /welche Anteil der Elemente besitzen höchstens die Merkmalswert X_i. Die Summenhäufigkeitsfunktion hat das Bild einer “Treppenfunktion”. Wenn aber die Ausprägung stetig ist oder wenn der Anzahl der diskreten Merkmalswerte sehr viel ist, dann es ist besser und leichter zu rechnen mit den klassifizierten Daten.

Häufigkeitsverteilung der klassifizierter Daten (sınıflı seri)

Nr. i	Examensnoten Klassen	Klassenbreite	Anzahl der Noten fi	Anteil in der Klasse pi
1	0-2	2	0	0.000
2	2-4	2	7	0.175
3	4-6	2	16	0.400
4	6-8	2	12	0.300
5	8-10	2	5	0.125
	Summe S		40	1.000

Bei der Klasseneinteilung wird das Ziel verfolgt, die Struktur der untersuchten Gesamtheit möglichst deutlich herauszuarbeiten. Selbst bei umfangreichem Datenmaterial sollte die Zahl der Klassen 20 nicht übersteigen. Man kann konstante oder unterschiedliche Klassenbreite verwenden. Die obere Klassengrenze gehört zu der Klasse weil die untere nicht.

2.2.3 Zentrale Tendenz

Die zentrale Tendenz einer Verteilung ist eine Schätzung der "Mitte" einer Verteilung von Werten. Es gibt drei Haupttypen Schätzungen der zentralen Tendenz:

· Mittel

· Mittlere

· Modus

Das Mittel- oder das durchschnittliche ist vermutlich die am geläufigsten verwendete Methode des Beschreibens der zentralen Tendenz. Das Mittel alles zu berechnen, das Sie ist hinzufügen oben alle Werte und sich teilen durch die Zahl Werten. Z.B. wird die Mittel- oder durchschnittliche Quizkerbe festgestellt, indem man alle Kerben summiert und durch die Zahl den Kursteilnehmern sich teilt, welche die Prüfung nehmen. Z.B. betrachten Sie die Testkerbewerte:

15, 20, 21, 20, 6, 15, 25, 15

Die Summe dieser 8 Werte ist 167, also ist das Mittel 167/8 = 20.875.

Der Mittelpunkt ist die Kerbe, die an der genauen Mitte des Sets von Werten gefunden wird. Ein Weg zum Berechnen den Mittelpunkt soll alle Kerben in zahlenmäßiger Reihenfolge ausdrucken und lokalisiert dann die Kerbe in der Mitte der Probe. Z.B. wenn es 500 Kerben in der Liste gibt, würde Kerbe #250 der Mittelpunkt sein. Wenn wir die 8 Kerben bestellen, die oben gezeigt werden, würden wir erhalten:

15.15.15.20.20.21.25.36

Es gibt 8 Kerben und Kerbe #4 und #5 stellt den halben Punkt dar. Da beide dieser Kerben 20 sind, ist der Mittelpunkt 20. Wenn die zwei mittleren Kerben unterschiedliche Werte hatten, würden Sie interpolieren müssen, um den Mittelpunkt festzustellen.

Der Modus ist der am häufigsten auftretende Wert im Set der Kerben. Um den Modus festzustellen, konnten Sie die Kerben wieder bestellen wie oben gezeigt und zählen dann jedes. Der am häufigsten auftretende Wert ist der Modus. In unserem Beispiel tritt der Wert 15 dreimal auf und ist das Modell. In etwas Verteilungen gibt es mehr als einen modalen Wert. Zum Beispiel in einer mit zwei Verfahrenverteilung gibt es zwei Werte, die am häufigsten auftreten.

Beachten Sie, daß für das gleiche Set von 8 Kerben wir drei unterschiedliche Werte -- 20.875, 20 und 15 -- für das Mittel, den Mittelpunkt und den Modus beziehungsweise erhielten. Wenn die Verteilung wirklich (d.h., glockenförmig) normal ist, das Mittel, Mittelpunkt und aller Modus sind Gleichgestelltes miteinander.

Arithmetisches Mittel:

Weil die einzelnen Merkmalswerte Xi bei Vorliegen einer Häufigkeitsverteilung mit den absoluten bzw. relativen Häufigkeiten gewichtet, bezeichnet man m hier als gewogenes arithmetisches Mittel.

2.2.4 Zerstreuung

Zerstreuung spricht die Verbreitung der Werte um die zentrale Tendenz an. Es gibt zwei geläufige Masse Zerstreuung, Strecke und Standardabweichung. Die Strecke ist einfach der höchste Wert minus des niedrigsten Wertes. In unserer Beispielverteilung ist der hohe Wert 6 und das Tief ist 15, also ist die Strecke 6 - 15 = 21.

Die Standardabweichung ist eine genauere und ausführlichere Schätzung der Zerstreuung, weil eine Ausreißerdose groß die Strecke übertreiben (wie in diesem Beispiel in dem der einzelne Ausreißerwert von 6 Standplätzen abgesehen von dem Rest der Werte zutreffend. Die Standardabweichung stellt dar, daß die Relation, die von den Kerben einstellen, das Mittel der Probe muß. Lässt wieder Nehmen das Set der Kerben:

15.20.21.20.36.15.25.15

um die Standardabweichung zu berechnen, finden wir zuerst den Abstand zwischen jedem Wert und dem Mittel. Wir wissen von oben genanntem, daß das Mittel 20.875 ist. So sind die Unterschiede vom Mittel:

15 - 20.875 = -5.875
20 - 20.875 = -0.875
21 - 20.875 = +0.125
20 - 20.875 = -0.875
6 - 20.875 = 15.125
15 - 20.875 = -5.875
25 - 20.875 = +4.125
15 - 20.875 = -5.875

Beachten Sie, daß Werte, die unterhalb des Mittels sind, negative Diskrepanzen und Werte über ihm haben, Positiv zu haben eine. Zunächst quadrieren wir jede Diskrepanz:

-5.875 * -5.875 = 34.515625
-0.875 * -0.875 = 0.765625
+0.125 * +0.125 = 0.015625
-0.875 * -0.875 = 0.765625
15.125 * 15.125 = 228.765625
-5.875 * -5.875 = 34.515625
+4.125 * +4.125 = 17.015625
-5.875 * -5.875 = 34.515625

Jetzt nehmen wir diese "quadrieren" und summieren sie, um die Summe des Wertes der Quadrate (SS) zu erhalten. Hier ist die Summe 350.875. Zunächst teilen wir diese Summe durch die Zahl Kerben minus 1. Hier ist das Resultat 350.875/7 = 50.125. Dieser Wert bekannt als die Abweichung. Um die Standardabweichung zu erhalten, nehmen wir die Quadratwurzel der Abweichung (erinnern Sie daran daß wir die Abweichungen früh quadrierten). Dieses würde SQRT(50.125) = 7.079901129253 sein.

Obgleich wir diese univariate Statistiken eigenhändig errechnen können, erhält es ziemlich langwierig, wenn Sie mehr als einige Werte und Variablen haben. Jedes Statistikprogramm ist zu sie leicht errechnen für Sie fähig. Zum Beispiel setzte ich die acht Kerben in SPSS und erhielt die folgende Tabelle infolgedessen:

N	8
Mean	20.8750
Median	20.0000
Mode	15.00
Std. Deviation	7.0799
Variance	50.1250
Range	21.00

Die Standardabweichung erlaubt uns, einige Zusammenfassungen über spezifische Kerben in unserer Verteilung zu erreichen. Annehmen, daß die Verteilung der Kerben normal oder glockenförmig ist (oder nah an ihr!), die folgenden Zusammenfassungen können erreicht werden:

· ungefähr 69% der Kerben im Beispielfall innerhalb einer Standardabweichung des Mittel

· ungefähr 95% der Kerben im Beispielfall innerhalb zwei Standardabweichungen des Mittel

· ungefähr 99% der Kerben im Beispielfall innerhalb drei Standardabweichungen des Mittels

Zum Beispiel da das Mittel in unserem Beispiel 20.875 ist und die Standardabweichung 7.0799 ist, wir Dose von der oben genannten Anweisungschätzung, daß ungefähr 95% der Kerben in die Strecke 20.875-(2*7.0799) bis 20.875+(2*7.0799) oder zwischen 6.7152 und 35.0348 fällt. Diese Art der Informationen ist ein kritischer Tretenstein zum Aktivieren wir, die Leistung einer Einzelperson auf einer Variable mit ihrer Leistung auf anderen zu vergleichen, selbst wenn die Variablen auf völlig unterschiedlichen Skalen gemessen werden.

2.2.5 Korrelation

Die Korrelation ist eine der geläufigsten und meisten nützlichsten Statistiken. Eine Korrelation ist eine einzelne Zahl, die den Grad des Verhältnisses zwischen zwei Variablen beschreibt.

Sie sollten in den zweidimensionalen Plot sofort sehen, daß das Verhältnis zwischen den Variablen ein positives ist (wenn Sie nicht das sehen können, das Kapitel auf Typen von Verhältnissen wiederholen Sie), weil, wenn Sie eine einzelne gerade Geraden durch die Punkte passen sollten, die sie eine positive Steigung haben oder von links nach rechts hochschiebt würde.  Da die Korrelation nichts mehr als eine quantitative Schätzung des Verhältnisses ist, würden wir eine positive Korrelation erwarten.

Was ein Mittel "des positiven Verhältnisses" in diesem Kontext? Es bedeutet, daß, im allgemeinen, höhere Kerben auf einer Variable neigen, mit höheren Kerben auf der anderen zusammengepasst zu werden und daß unterere Kerben auf einer Variable neigen, mit untereren Kerben auf der anderen zusammengepasst zu werden. Sie sollten sichtlich bestätigen, daß dieses im Allgemeinen im Plot oben zutreffend ist.

Man verwendet das Symbol r Um für die Korrelation zu stehen. Durch die Magie von Mathematik fällt sie aus, daß r immer zwischen -1.0 und +1.0 ist. Wenn die Korrelation negativ ist, haben wir ein negatives Verhältnis; wenn sie positiv ist, ist das Verhältnis positiv.

Sobald Sie eine Korrelation berechnet haben, können Sie die Wahrscheinlichkeit feststellen, daß die beobachtete Korrelation zufällig auftrat. Das heißt, können Sie einen Signifikanzstest leiten. Häufig sind Sie interessiert, an, die Wahrscheinlichkeit festzustellen, daß die Korrelation ein reales und nicht ein zufälliges Auftreten ist. In diesem Fall prüfen Sie die gegenseitig Exklusivhypothesen:

· ungültige Hypothese: r = 0

· alternative Hypothese: r ¹ 0

Die einfachste Methode, diese Hypothese zu prüfen soll finden Statistiken anmelden, die eine Tabelle der kritischen Werte von r hat. Die meisten einleitenden Statistiktexte würden eine Tabelle so haben. Wie in aller prüfenden Hypothese, müssen Sie die Signifikanzstufe zuerst feststellen. Hier benutzt man die geläufige Signifikanzstufe a= 0.05. Dies heißt, daß ich einen Test leite, in dem die Vorteile, daß die Korrelation ist ein zufälliges Auftreten nicht mehr als 5 aus 100 heraus ist. Bevor ich oben den kritischen Wert in einer Tabelle auch schaue, müssen die Freiheitsgrade oder DF berechnen. Das DF ist gleich N-2. Schließlich muß ich entscheiden, ob ich einen ein-einseitigen oder zweischwänzigen Test durchführe. In diesem Beispiel da ich keine starke vorherige Theorie habe, zum vorzuschlagen, ob das Verhältnis zwischen Höhe und Selbstachtung positiv oder negativ sein- würde, entscheide ich für den zweischwänzigen Test. Mit dieser drei Information -- die Signifikanzniveau (Alpha = 05)), Freiheitsgrade und Typ des Tests (zweischwänzig) -- kann man die Signifikanz der Korrelation jetzt prüfen. Zum Beispiel, wenn ich oben diesen Wert in der handlichen kleinen Tabelle der Rückseite meiner Statistiken betrachte, melden Sie mich finden an, daß der kritische Wert 0.4438 ist. Dies heißt, daß, wenn meine Korrelation grösser als 0.4438 oder weniger als -.4438 ist (erinnern Sie sich, dieses ist ein zweischwänziger Test), kann ich feststellen, daß die Vorteile kleiner als 5 aus 100 heraus sind, daß dieses ein zufälliges Auftreten ist. Da mein Korrelation 0.73 wirklich durchaus ein wenig stark ist, stelle ich fest, daß es nicht eine Wahrscheinlichkeit ist, die findet und daß die Korrelation "statistisch bedeutend" ist (die Parameter des Tests gegeben). Ich kann die ungültige Hypothese zurückweisen und die Alternative annehmen.

Der spezifische Typ der Korrelation, die ich hier veranschaulicht habe, bekannt als die Pearson Produkt-Moment-Korrelation. Es ist angebracht, wenn beide Variablen auf einer Abstand Stufe gemessen werden. Jedoch es gibt eine breite Vielzahl anderer Typen Korrelationen für andere Umstände. zum Beispiel wenn Sie zwei Ordnungsvariablen haben, konnten Sie die Spearman-Rangfolge-Korrelation (Rho) oder die Kendall Rangfolge Korrelation (tau) verwenden. Wenn ein Maß eine ununterbrochene Abstand Stufe eine und ist, ist anderes (d.h., Zweikategorie) Sie kann die Punkt-Biserial Korrelation verwenden dichotomous.

2.3 Induktiven Statistik

Mit induktiven Statistiken versuchen Sie, Zusammenfassungen zu erreichen, die über den Direktdaten hinaus alleine sich ausdehnen. Zum Beispiel verwenden wir gefolgerte Statistiken, um zu versuchen, von den Beispieldaten zu schließen, was die Bevölkerung denken konnte. Oder, wir verwenden gefolgerte Statistiken, um Urteile von der Wahrscheinlichkeit zu bilden, daß ein beobachteter Unterschied zwischen Gruppen ein zuverlässiges oder eins ist, die zufällig in dieser Studie geschehen sein konnten. So verwenden wir gefolgerte Statistiken, um Folgerungen von unseren Daten zu den allgemeineren Bedingungen zu bilden; wir verwenden beschreibende Statistiken einfach, um zu beschreiben, was an in unsere Daten geht.

Hier konzentriere mich ich auf gefolgerte Statistiken, die im experimentellen und quasi-experimentellen Forschung Design oder in der Programmresultat Auswertung nützlich sind. Möglicherweise ein des einfachsten induktiven Tests wird verwendet, wenn Sie die durchschnittliche Leistung von zwei Gruppen auf einem einzelnen Maß vergleichen möchten, zu sehen, wenn es einen Unterschied gibt. Sie konnten wissen wünschen, ob Achtgrad Jungen und Mädchen in den Mathetestkerben sich unterscheiden, oder ob eine Programmgruppe auf dem Resultat Maß von einer Steuergruppe sich unterscheidet. Wann immer Sie die durchschnittliche Leistung zwischen zwei Gruppen vergleichen möchten, sollten Sie den Ttest für Unterschiede zwischen Gruppen betrachten.

Die meisten induktiven hauptsächlichstatistiken kommen von einer allgemeinen Familie der statistischen Modelle, die als das allgemeine lineare Modell bekannt sind.Dieses enthält den Ttest, Varianzanalyse (ANOVA), Analyse der Kovarianz (ANCOVA), Regressionanalyse und viele der multivariaten Methoden wie Faktoranalyse, mehrdimensionale Skalierung, Clusteranalyse, diskriminierende Funktion Analyse und so weiter. Den Wert des allgemeinen linearen Modells gegeben, ist es eine gute Idee, damit jeder ernste Sozialforscher mit seinen Funktionen vertraut wird. Die Diskussion über das allgemeine lineare Modell hier ist sehr grundlegend und betrachtet nur das einfachste lineare Modell. Jedoch erhält sie Sie vertraut mit der Idee des linearen Modells und hilft, Sie für die komplizierteren unten beschriebenen Analysen vorzubereiten.

Eine der Tasten zum Verstehen, wie Gruppen verglichen werden, wird im Begriff der "blinden" Variable dargestellt. Der Name schlägt nicht vor, daß wir Variablen, die nicht sehr intelligent sind oder, gleichmäßiges falscheres verwenden, daß der Analytiker, der sie verwendet, ist eine "Attrappe"! Möglicherweise würden diese Variablen besser als "Vollmacht" Variablen beschrieben. Im Wesentlichen ist eine Platzhaltervariable ein, die getrennte Zahlen verwendet, normalerweise 0 und 1, unterschiedliche Gruppen in Ihrer Studie darzustellen. Platzhaltervariablen sind eine einfache Idee, die einige hübsche schwierige Sachen aktivieren zu geschehen. Zum Beispiel indem ich eine einfache Platzhaltervariable in einem Modell einschließe, kann ich zwei verschiedene Zeilen (eine für jede Behandlunggruppe) mit einer einfachen Gleichung formen. Sehen, wie dieses arbeitet, aus der Diskussion auf Platzhaltervariablen überprüfen.

Eine der wichtigsten Analysen in den Programmresultat Auswertungen bezieht mit ein, die Programm- und Nichtprogrammgruppe auf der Resultat Variable oder den Variablen zu vergleichen. Wie wir tun, hängt dieses vom Forschung Design ab, das wir Forschung Designs werden geteilt in zwei Haupttypen Designs verwenden: experimentell und quasi-experimentell.Weil die Analysen für jedes sich unterscheiden, werden sie separat dargestellt.

Experimentelle Analyse.Das einfache Zweigruppe posttest-only randomisierte Experiment wird normalerweise mit dem einfachen Ttest oder dem Einweg-ANOVA analysiert. Die Faktoren- experimentellen Designs werden normalerweise mit der Varianzanalyse (ANOVA) Modell analysiert. Randomisierte Blockbauweisen benutzen ein spezielles Formular von ANOVA, das Modell blockt, das blind-codierte Variablen verwendet, um die Blöcke darzustellen. Die Analyse Kovarianz-des experimentellen Design- Gebrauches, nicht überraschend, die Analyse des statistischen Modells der Kovarianz.

Quasi-Experimentelle Analyse.Die quasi-experimentellen Designs unterscheiden sich von den experimentellen dadurch, daß sie nicht gelegentliche Anweisung verwenden Um Maßeinheiten (z.B., Leute) Programmgruppen zuweisen. Der Mangel an gelegentlicher Anweisung in diesen konzipiert neigt, ihre Analyse beträchtlich zu erschweren. Z.B. Um das antivalente Gruppen Design (NEGD) zu analysieren müssen wir einstellen die Voruntersuchungkerben auf Messfehler in, was häufig eine Zuverlässigkeit-Behobene Analyse des Kovarianzmodells genannt wird. Im Regression-Unstimmigkeit Design müssen wir über curvilinearity und Modellmangelhafte Spezifikation besonders betroffen werden. Infolgedessen neigen wir, eine konservative Analyse Annäherung zu verwenden, die auf polynomischer Regression basiert, die Anfänge, indem sie die wahrscheinliche zutreffende Funktion overfitting und dann das Modell verringerten, auf den Resultaten gründeten. Das Regression-Punkt-Distanzadresse-Design hat nur eine einzelne behandelte Maßeinheit. Dennoch basiert die Analyse des RPD Designs direkt auf dem traditionellen ANCOVA Modell.

Wenn Sie diese verschiedenen analytischen Modelle nachgeforscht haben, sehen Sie daß sie alle, von der gleichen Familie zu kommen -- das allgemeine lineare Modell.Ein Verständnis dieses Modells geht ein langer Weg zum Vorstellen Sie zu den Verwicklungen der Datenanalyse in angewandten und Sozialforschung Kontexten.

2.4 Formulierung und Überprüfung von Hypothesen

Statistische Kennwerte erlauben es, eine Stichprobe durch ihre Lageparameter und ihre Streuung zu beschreiben. Dient der statistische Test zur Überprüfung einer Hypothese über unbekannte Parameter der Grundgesamtheit (m, p, s²), so handelt es sich um einen parametrischen Test. Soll die unbekannte Verteilung einer Grundgesamtheit überprüft werden, so sind Verteilungstests (nicht parametrische Tests) heranzuziehen. Die durch den Test zu überprüfende Hypothese ist die Nullhypothese Ho. Die Gegenannahme zur Behauptung der Nullhypothese wird in der Alternativhypothese Ha formuliert. Dabei wird mitunter empfohlen, dab Ha den eigentlich interessierenden Tatbestand enthält. Das Testverfahren soll sicherstellen, dab die Wahrscheinlichkeit eines Einführungsrisiko (a-Fehler) und zugleich eines Gewinnensgangsrisiko (b-Fehler) in sinnvollen Grenzen gehalten werden.

Entscheidung aufgrund	in der Grundgesamtheit gilt:
der Stichprobe	Ho trifft zu	Ho trifft nicht zu
Ho nicht abgelehnt	Richtige Entscheidung	b-Fehler
Ho abgelehnt	a-Fehler	Richtige Entscheidung

2.4.1 Beispiele für Hypothese

· Die Einführung einer neu entwickelten Produktvariante würde sich nur lohnen, wenn ein höherer Marktanteil als 10% erzielt wird. Ho:p£0.10, Ha:p>0.10. (Bereichshypothese)

· Die Einführung einer neu entwickelten Produktvariante würde sich nur in einer Stadt lohnen, wenn mittlere Einkommen 10000 DM ist. Ho:m=10000, Ha:m¹10000. (Punkthypothese)

Hier wird einige wichtige Testverfahren zusammengefassten. (v: Freiheitsgraden)

Nullhypothese	Kenntnis über Grundgesamtheit	Anzuwendende Verteilung	Bedingung
m=mo	s bekannt	z	Grundgesamtheit normalverteilt oder n>30
m=mo	s unbekannt	t, v=n-1	Grundgesamtheit normalverteilt
p=po		z	np(1-p)³9
s^2=so^2		c^2, v=n-1	Grundgesamtheit normalverteilt
m1=m2	s1, s2 bekannt	z	Grundgesamtheit normalverteilt oder n1,n2>30
m1=m2	s1, s2 unbekannt, s1¹s2	z	n1,n2>30
m1=m2	s1, s2 unbekannt, s1=s2	t, v=n1+n2-2	Grundgesamtheiten normalverteilt
p1=p2		z	n1p1(1-p1)³9, n2p2(1-p2)³9
s^21=s^22		F, v1=n1-1, v2=n2-1	Grundgesamtheiten normalverteilt
m2i=m1i+d	i=1,2,...,n; d=0	t, v=n-1	Grundgesamtheiten normalverteilt
m1=m2=.....=mk		F, vA=k-1, vR=nk-k	Grundgesamtheiten normalverteilt und homogen s1=s2=.....=sk
Anpassungstest	k: Zahl der Klassen, m:Zahl der geschätzten Parameter	c^2, v=k-m-1	E(fi)³5
Anpassungstest	Kolmogorov-Smirnov	K-S Prüfgröbe
2 Merkmale sind unabhängig voneinander	r,s: Anzahl der Merkmalsausprägungen	c^2, v=(r-1)(s-1)	E(fij)³5
Homogenitätstest	r: Anzahl der Ausprägung s: Anzahl der Stichproben	c^2, v=(r-1)(s-1)	E(fij)³5
s^21=s^22=.......=s^2k	Levene Homogenitätstest	F	Grundgesamtheiten normalverteilt
r=0, r=r0	Pearson Korrelation	t, v=n-2	Grundgesamtheiten normalverteilt
r=0	Spearman Korrelation	Spearman Prüfgröße	Zufallsauswahl, kontinuierliche Verteilung
bi=0	Regressionskoeffizienten	t, v=n-k	Bedingungen für Regressionsanalyse

Dabei empfiehlt sich bei der Abwicklung des Tests folgende Reihenfolge:

10. Formulierung der Hypothesen,

11. Wahl des geeigneten Tests,

12. Festlegung des Signifikanzniveaus (a),

13. Bestimmung des kritischen (aus der Tabelle) Wertes der Prüfgröße,

14. Berechnung des empirischen Wertes der Prüfgröße (Teststatistik),

15. Vergleich der Prüfgrößen und Entscheidung.

2.4.2 Nicht parametrische Verteilungen und Hypothesenüberprüfung

Es gibt alternative nicht parametrische Methoden zu den parametrischen Tests. Diese Methoden haben auch einige Bedingungen. Diese Bedingungen sind dab die Stichproben zufällig und unabhängig voneinander ausgewählt sind. Die Teststatistik dieser nicht parametrischen Verteilungen berechnet man nicht durch die Merkmalsausprägungen (Zahlen), sondern durch die Rangordnung. Die folgende tabellarische Darstellung zeigt diese Methoden mit der Vergleichung den parametrischen Methoden. Außerdem, die schon beschreibenden Chi-Quadrat Unabhängigkeit-, Anpassungs-, Homogenitätstests und Kolmogorov-Smirnov Anpassungstest sind nicht parametrische Prüfgrößen.

		Differenzen
Skalen-niveau	Univariate	2 unabhängige	2 abhängige	k- unabhängige	k- abhängige
Verhältnis oder Intervall	t-, z-test von Lageparameter	t-, z-test von Lageparameter	t-test	Varianzanalyse ANOVA
Ordinal	Sign-test, c^2, K-S	Mann-Whitney-U, K-S-Z	Wilcoxon, Sign, McNemar	Median, Kruskal-Wallis-H	Friedman, Kendall’s W, Cochran’s Q
Nominal		c^2 Homgenität	c^2 Unabhängigkeit	c^2 Homogenität
Dichotom	t-test von Anteil	z-t-test von Anteil	Phi-Koeffizient

2.4.1 P Werte und Statistische Signifikanz

Sie benötigt traditionelle Annäherung an das Berichten über ein Resultat Sie, zu sagen, ob es statistisch bedeutend ist. Sie sollen es tun, indem man einen p Wert von einer Test statistik festlegt. Sie zeigen dann ein bedeutendes Resultat mit "p<0.05" an. Lassen Sie so uns herausfinden was dieses p ist, was spezielles ungefähr 0.05istund wann man mit P., das ich auch die in Verbindung stehenden Themen von ein-angebunden gegen zweischwänzige Tests beschäftigeund die Hypothese prüfung benutzt.

P ist für Wahrscheinlichkeit kurz: die Wahrscheinlichkeit des Erhaltens etwas extremer als Ihr Resultat, wenn es keinen Effekt in der Grundgesamtheit gibt. Seltsam! Und was ist dieses, das erhalten wird, um mit statistischer Signifikanz zu tun? Lassen Sie uns sehen.

Ich habe bereits statistische Signifikanz in Vertrauen Abständen ausgedrückt definiert. Das andere Annäherung an statistische Signifikanz -- die, die p Werte miteinbezieht -- ist ein gewundenes Bit. Zuerst nehmen Sie an, daß es keinen Effekt in der Grundgesamtheit gibt. Dann sehen Sie, wenn der Wert, den Sie für den Effekt in Ihrer Probe erhalten, die Sortierung des Wertes ist Sie für keinen Effekt in der Grundgesamtheit erwarten würden. Wenn der Wert, den Sie erhalten, für keinen Effekt unwahrscheinlich ist, folgern Sie dort sind ein Effekt, und Sie Sagen das Resultat sind "statistisch bedeutend".

Lassen Sie uns ein Beispiel nehmen. Sie sind an der Wechselbeziehung zwischen zwei Sachen interessiert, sagen Höhe und Gewicht und Sie haben eine Probe von 20 Themen. HEISSEN Sie gut, nehmen Sie an, daß es keine Wechselbeziehung in der Grundgesamtheit gibt. Jetzt sind was etwas unwahrscheinliche Werte für eine Wechselbeziehung mit einer Probe von 20? Hängt ab, was wir durch "unwahrscheinliches" bedeuten. Lassen Sie uns es Mittel "extreme Werte, 5% bilden der Zeit". In diesem Fall mit 20 Themen, treten alle Wechselbeziehungen, die oder negativer als -0.44 positiver als 0.44 sind, nur 5% der Zeit auf. Was erhielten Sie in Ihrer Probe? 0.25? O.K., das ist nicht ein unwahrscheinlicher Wert, also ist das Resultat nicht statistisch bedeutend. Oder wenn Sie -0.63 erhielten, würde das Resultat statistisch bedeutend sein. Einfach!

Aber warten Sie eine Minute. Was über den p Wert? Das Problem ist, daß Statistik Programme Ihnen die Schwellenwerte nicht geben, ±0.44 in unserem Beispiel. Die ist die Methode, die es verwendete , vor Computern getan zu werden. Sie schauten oben eine Tabelle der Schwellenwerte nach Wechselbeziehungen oder nach irgendeiner anderer Statistik, um, ob Ihr Wert mehr oder weniger als der Schwellenwert war, für Ihre Mustergröße zu sehen. Statistik Programme konnten sie tun so, aber sie nicht. Sie wünschen die Wechselbeziehung, die einer Wahrscheinlichkeit von 5% entspricht, aber das Statistik Programm gibt Ihnen die Wahrscheinlichkeit, die Ihrer beobachteten Wechselbeziehung -- das heißt, die Wahrscheinlichkeit von etwas entspricht, das, entweder Positiv oder Negativ extremer als Ihre Wechselbeziehung ist. Der ist der p Wert. Ein wenig Gedanke erfüllt Sie, das, wenn der p Wert kleiner als 0.05 (5%) ist, Ihre Wechselbeziehung als der Schwellenwert grösser sein muß, also ist das Resultat statistisch bedeutend. Für eine beobachtete Wechselbeziehung von 0.25 mit 20 Themen, würde ein Statistik Paket einen p Wert von 0.3 zurückbringen. Die Wechselbeziehung ist folglich nicht statistisch bedeutend.

Hier ist unser Beispiel, das in einem Diagramm zusammengefaßt wird:

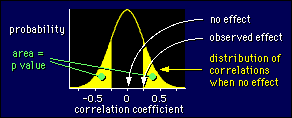
Die Kurve zeigt die Wahrscheinlichkeit des Erhaltens eines bestimmten Wertes der Wechselbeziehung in einer Probe von 20, wenn die Wechselbeziehung in der Grundgesamtheit null ist. Für einen bestimmten beobachteten Wert sagen Sie 0.25, wie gezeigt, der p Wert die Wahrscheinlichkeit des Erhaltens allem grösser als 0.25 und allem weniger als -0.25 ist. Diese Wahrscheinlichkeit ist die Summe der schraffierten Bereiche unter der Wahrscheinlichkeit Kurve. Es ist ungefähr 30% des Bereiches oder ein p Wert von 0.3. (das ganze Gebiet unter einer Wahrscheinlichkeit Kurve ist 1 oder absolute Sicherheit, weil Sie einen Wert irgendeiner Art erhalten müssen.)

Fallend in das resultiert, schraffierter Bereich sind nicht genau unwahrscheinlich, sind sie? Nr., benötigen wir einen kleineren Bereich, bevor wir über das Resultat aufgeregt erhalten. Normalerweise ist es ein Bereich von 5% oder ein p Wert von 0.05. Im Beispiel würde das für Wechselbeziehungen grösser als 0.44 oder weniger als -0.44. geschehen, also würde eine beobachtete Wechselbeziehung von 0.44 (oder von -0.44) einen p Wert von 0.05 haben. Grössere Wechselbeziehungen würden sogar kleinere p Werte haben und würden statistisch bedeutend sein.

2.5 Multivariete Analysen

Manchmal, Variablen mit verschiedenen Skalenniveau wurden zusammen bearbeitet. Die folgende Einteilung zeigt die Verfahren zur Dependenzanalyse. Man soll nicht vergessen dab die darunter gegebene Methoden einige Bedingungen haben, worüber bewusst sein soll.

Variablen	Kriteriumsvariable
	Skalenniveau	Nominal	Metrisch
Prädiktor- variable(n)	Nominal	Kreuztabellierung Kontingenzanalyse	Varianzanalyse
	Metrisch	Diskriminanz Analyse	Regressionsanalyse

2.5.1 T Test und Einweg-ANOVA

In andere Wörter, wenn Sie jemand Geschlecht wissen, was erklärt das Ihnen über ihre Höhe? Oder, wie gut fallen die Höhe Daten in zwei Gruppen, wenn Sie die Werte durch Geschlecht beschriften? Die Teststatistik für den Test von, ob Geschlecht einen Effekt auf Höhe hat, wird Student-t. Folglich der Name dieses Modells, der t Test benannt.

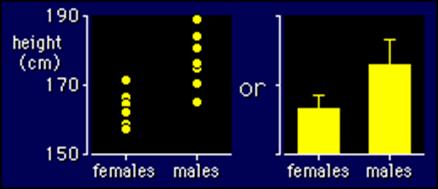
Wenn es drei oder mehr Stufen für die nominale Variable gibt, soll eine einfache Annäherung eine Reihe t Tests zwischen alle Paare der Stufen laufen lassen. Z.B. konnten wir an den Höhen der Athleten in drei Sport interessiert sein, also könnten wir t Test für jedes Paar Sport laufen lassen. (Anmerkung, daß diese Annäherung nicht dieselbe wie ein Abhängige t-Test ist. Das kommt später.) Eine leistungsfähigere Annäherung soll alle Daten in einem analysieren gehen. Das Modell ist dasselbe, aber es wird jetzt eine Einwegvarianzanalyse (ANOVA) genannt, und die Teststatistik ist das F Verhältnis. So sind t Tests ein spezieller Fall von ANOVA gerecht: wenn Sie die Mittel von zwei Gruppen durch ANOVA analysieren, erhalten Sie die gleichen Resultate wie, es mit einem t Test tuend.

Die Bezeichnung Varianzanalyse ist eine Quelle des Durcheinanders für Neue. Trotz seines Namens wird ANOVA mit Unterschieden zwischen Mitteln der Gruppen, nicht Unterschiede zwischen Abweichungen betroffen. Die Namensvarianzanalyse kommt von der Methode, welche die Prozedur Abweichungen verwendet, um zu entscheiden, ob die Mittel unterschiedlich sind. Ein besseres Akronym für dieses Modell würde ANOVA’s MAD sein (Varianzanalyse, zum zu sehen, wenn Mittel unterschiedlich sind)! Die Methode, die es funktioniert, ist einfach: das Programm schaut, um zu sehen was die Variante (Abweichung) innerhalb der Gruppen ist, ausarbeitet dann, wie diese Variante in Variante (d.h. Unterschiede) zwischen den Gruppen übersetzen würde und in Betracht zieht, wie viele Themen dort in den Gruppen sind. Wenn die beobachteten Unterschiede viel größer als sind, was Sie zufällig erwarten würden, haben Sie statistische Signifikanz. In unserem Beispiel gibt es nur zwei Gruppen, also ist Variante zwischen Gruppen der Unterschied zwischen den Mitteln gerecht.

2.5.2 Kontingenz Tabelle und Chi-Quadrant Test

Welchen Effekt hat das Geschlecht eines Zickleins auf der Art des Sports s/he mag? Die ist die Sortierung der Frage, die wir mit diesem Modell adressieren, wie im Beispiel der Sportpräferenzen einer Probe der Jungen und der Mädchen gezeigt.

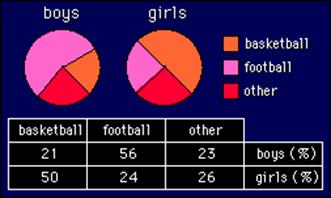
Die Wort Kontingenz verweist im Namen des Modells zum Verhältnis zwischen den zwei Variablen. Tabelle spricht für sich. Der Test für, ob es irgendein Verhältnis an allen gibt, bekannt als der Chi-Quadrat Test, von der Teststatistik, das quadrierte Chi (c2).Es liegt recht auf der Hand, daß es ein starkes Verhältnis im Beispiel gibt. Ob das Verhältnis bedeutend ist, würde von der Zahl Jungen und Mädchen abhängen.

Wir nicht normalerweise denken an Parameter für dieses Modell, aber sie würden die Wahrscheinlichkeiten des Entscheidens für jeden Sport, für jedes Geschlecht sein. Güte des Sitzes wird auch nicht normalerweise errechnet, aber verschiedene Entsprechungen des Korrelationskoeffizienten (z.B. der Kappa Koeffizient) bilden ihr Aussehen gelegentlich. Jene Resultat Masse, die wir bereits getroffen haben, die relative Gefahr und das Vorteile Verhältnis, sind sinnvoll nur für 2 x 2 Tabellen oder für das Vergleichen von 2 x 2 Zellen in einer größeren Tabelle. Die meisten Statistik Programme können die Vertrauen Abstände für diese Resultat Masse errechnen

Wenn Sie mehr als zwei Reihen oder Spalten in der Tabelle (z.B. der drei Sport oben) haben, erklärt der Chi-Quadrat Test Ihnen, daß ob es irgendein Verhältnis gibt, aber es erklärt Ihnen, wo nicht die Unterschiede sind. Jetzt gerade wie wir Tests für die unterschiedlichen Stufen einer Gruppierensvariable in einem ANOVA paarweise durchführen können, wir Dose prinzipiell Test für Unterschiede zwischen Frequenzen der Männer und der Frauen in den Paaren Sport oder zwischen einem Sport und dem Rest oder was auch immer. Im oben genannten Beispiel ist es frei, daß die "andere" Kategorie sich nicht zwischen Geschlechtern unterscheidet (die wirklich ein Vergleich von "anderer" mit dem kombinierten Basketball und Fußball ist, wenn Sie an ihn denken), während jede anderen paarweise Vergleich aussehen wie es unterschiedlich sein konnten. Die lustige Sache ist, gibt es keine Tradition für das Tun so prüft paarweise in einer Möglichkeit Tabelle oder auf die Steuerung des Typen I Fehler, nicht, der ich von irgendwie weiß. Aller, den Leute, ist Zustand, ob es einen gesamten Effekt oder nicht gibt, dann schaut die Frequenzen in der Tabelle an und kommentiert an, wo die größten Unterschiede sind.

2.5.3 Lineare Regression

Wie Sie sehen können, schreien Daten für zwei Variablen wie Gewicht und Höhe heraus, um eine gerade Geraden zu haben, die durch sie gezeichnet wird. Die gerade Gerade erlaubt uns, irgendein Gewicht der Person von einem Wissen der Höhe dieser Person vorauszusagen. Offensichtlich ist die Vorhersage nicht vollkommen, also können wir auch, zu sagen, wie stark das lineare Verhältnis zwischen Gewicht und Höhe ist oder wie gut die gerade Gerade die Daten paßt (die Güte des Sitzes).

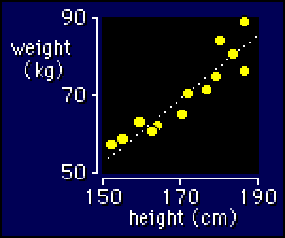
Ist hier, wie wir das Modell darstellen:

· Modell: numerisch < = numerisch

· Beispiel: Gewicht < = Höhe

Sie denken normalerweise an eine gerade Geraden als Y = MX + c, wo m die Steigung ist und c der Abschnitt ist. Die Methode würde ich dieses Verhältnis mit der oben genannten Darstellung, bin einfach Y < = X. We muß nicht um das Zeigen der Konstanten sich sorgen schreiben, aber das Statistik Programm sorgt sich um sie. Sie sind die Parameter im Modell.

Die Steigung

Er ist der meiste interessante Parameter in einem linearen Modell normalerweise die Steigung. Wenn die Steigung null ist, ist die Zeile, so dort ist kein Verhältnis zwischen den Variablen flach. Im Beispiel ist die Steigung ungefähr 0.75 Kilogramm pro Zentimeter (eine Zunahme des Gewichts von 0.75 Kilogramm für jede Zentimeter Zunahme der Höhe). Wir können die Steigung in zwei Möglichkeiten auch errechnen, die nicht jene häßlichen Maßeinheiten (Kilogramm pro Zentimeter) haben.

Ein Weg soll die Prozente errechnen ändern im Gewicht pro Prozente ändern in der Höhe. Er ist ungewöhnlich, aber manchmal ist es die beste Methode, besonders für Variablen, die Protokoll Transformation benötigen. Die Steigung, die als % pro % ausgedrückt wird, kommt direkt aus der Analyse der Protokoll-umgewandelten Variablen heraus.

Die andere Methode, die Maßeinheiten zu löschen soll die zwei Variablen, indem sie ihre Werte normalisieren durch ihre Standardabweichungen teilt, passte dann die gerade Geraden. Die resultierende Steigung bekannt als standardisierter Regressionskoeffizient. Sie stellt die Änderung im Gewicht dar, ausgedrückt als Bruch der Standardabweichung, pro Standardabweichungsänderung in der Höhe. Sie können sie auch festlegen, indem Sie die Steigung (in Kilogramm pro Zentimeter) mit dem Verhältnis der Standardabweichungen für Höhe über der Standardabweichung für Gewicht multiplizieren. In einer einfachen linearen Regression ist der Wert des standardisierten Regressionskoeffizienten genau derselbe wie der Korrelationskoeffizient, und Sie können seine Größe in der gleichen Methode deuten. Bezüglich des Beispiels ist der Wert ungefähr 0.9 oder ein Unterschied von 0.9 Standardabweichungen im Gewicht pro Änderung von einer Standardabweichung in der Höhe. Das ist ein wirklich starkes Verhältnis.

2.5.4 Kategorische Formung

In ein anderer Name für dieses Modell ist diskriminierende Funktionsanalyse, weil z.B. Sie oben mit einer Funktion beenden der Höhe, die erlaubt Ihnen, vorauszusagen, welchem Sport eine Person gehört. Ob die Person besser dadurch tun würde, daß Sport eine andere Frage ist, die unterschiedliche Variablen benötigt, selbstverständlich!

Dieses Modell ist das wenige Common der vier. Es ist viel einfacher, das Modell herum zu drehen, um es Höhe zu bilden < = Sport und trifft… zu, was? Ja ein ANOVA. Ausschließlich sprechend, obwohl, wenn die Forschung Höhe verlangt, um die unabhängige Variable zu sein, dann sollten Sie die kategorische Formung anwenden und Ihre Resultate als Effekt der Höhe auf der Wahrscheinlichkeit des Seins im unterschiedlichen Sport ausdrücken. Sie beenden oben mit schrecklichen Resultat Massen wie einem Vorteile Verhältnis pro Maßeinheit der Höhe, die weg jeder ausgenommen Karte-tragende Statistiker durchbrennt! Übrigens wird die Teststatistik Chi-Quadrat.

Ein spezieller Fall kategorischer Formung ist logistische Regression. Sie müssen dieses Modell benutzen, wenn die abhängige Variable ordinal ist. Sie können nicht sie zu ein ANOVA herum machen.

2.5.5 Hauptkomponentenanalyse

Wenn Sie viele unterschiedliche Messen in einer Studie nehmen, möchten Sie manchmal sie auf gewisse Weise kombinieren, um gerade ein oder zwei Masse zu berechnen, die irgendeinen Aspekt der Daten zusammenfassen. Z.B. konnten Sie fünf unterschiedliche Masse der Körpergröße haben, aber möchten einfach ein oder zwei Zusammenfassung Maß haben, die die fünf kombinieren. Die zusammenfassenden Maßnahmen werden von der Analyse der Hauptkomponenten getroffen.

Alles, das Sie, ist erklären dem Statistik Programm, welche Variablen Sie es analysieren wünschen. Es kommt oben mit einer linearen Kombination der Variablen, die irgendwie die größte Menge der geläufigen Veränderung der alle erfasst. Es fährt dann fort, eine andere lineare Kombination zu produzieren, die die größte Menge von Veränderung erfasst, was gelassen wird und so. Wenn Sie mit drei Variablen beginnen, erhalten Sie drei allgemeine Bestandteile. Die nette Sache über sie ist, werden sie nicht mit einander aufeinander bezogen, also stellen sie drei total unabhängige Masse dar. Genau was sie in der Wirklichkeit darstellen, muss entschieden werden, indem man die belastenden Faktoren betrachtet, dass das Statistik Programm berechnet, um die allgemeinen Bestandteile zu bilden. Manchmal liegt es nicht auf der Hand, dass sie aussagefähiges alles darstellen und Sie diese Annäherung verlassen müssen konnten.

2.5.6 Faktor-Analyse

Hier wünschen Sie Kombinationen von Variablen mit dem gleichen Belasten, und Sie werden im Allgemeinen nicht betroffen, wenn die resultierenden Zusammensetzungen aufeinander bezogen werden. Diese Methode wird von den Psychologen (oder von ihren Statistikern) verwendet um eindeutige Maße der Psyche von den Teilmengen Einzelteilen in den Multieinzelteil Fragen zu berechnen. Faktoranalyse teilt die Einzelteile in Teilmengen so, daß Einzelteile mittendrin jede Teilmenge aber nicht so gut zwischen Teilmengen aufeinander beziehen. Jedes Thema erhält dann eine Mittelkerbe für die Einzelteile in jeder Teilmenge. Der Forscher muß was entscheiden, das Mittel zu benennen zählt, indem er die Ausdrucksweise der Einzelteile betrachtet.

Es ist einige Jahre, da ich Faktoranalyse tat, die ist, warum dieses Kapitel so kurz ist! Wenn es eine Nachfrage nach ihr gibt, schließe ich das Detail über solche Sachen wie promax Umdrehung und das Entscheiden ein, wo man die Zeile für Einbeziehung von Variablen in einem Faktor zeichnet.

2.5.7 Clusteranalyse

Dieses ist ein besonders strenges Formular der Maßverkleinerung, die alle Variablen und Daten unten auf einer Variable mit nur einigen Werten verringert (z.B. gruppieren Sie A, Gruppe B und Gruppe C). Zu verstehen ist am einfachsten, vom Beispiel in der Abbildung, die Höhen und

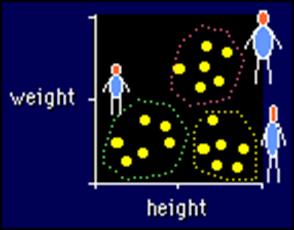
Gewichte für ein Bündel Leute zeigt, die offensichtlich in drei Gruppen oder "in Blöcke" fallen:

Sie können das Statistik Programm auf der Zahl Blöcken entscheiden lassen, oder Sie können sie erzwingen, um zu finden bis zu, wie Sie mögen. Das Programm entscheidet, welche Beobachtungen gehören, welchem Block durch die Minderung der Abstände zwischen Punkten in jedem Block. Sie werden nicht auf zwei Variablen, selbstverständlich eingeschränkt. Es ist unmöglich, sich Blöcke für mehr als drei Variablen vorzustellen (es sei denn Sie ein Einstein sind), aber das Statistik Programm handhabt es ohne irgendein Problem.

Clusteranalyse wird in der Marktforschung verwendet, in der Sie einige Hauptzielgruppen in einer Grundgesamtheit kennzeichnen möchten. Und es ist eine kühle Methode des Kennzeichnens der Gruppen in der Grundgesamtheit mit bestimmten Lebensstilen. Die Variablen, die in der Clusteranalyse verwendet wurden, konnten Alter, Geschlecht, sozioökonomischer Status, Stufe der körperlichen Aktivität, Masse von der Diät sein und so weiter.

3. Gehen von der Forschung Frage, zu Forschungsdesigns

Dieses Dokument behandelt die unterschiedlichen Typen der Forschung Fragen und beschreibt einige Grundlagenforschungsdesigns, die mit jedem Typen verwendet werden. Auch die allgemeinen Stärken und die Schwächen jedes Designs werden erklärt.

Sobald Sie das Muster haben, können Sie diese Tabelle benutzen, um das korrekte statistische Prüfen zu lokalisieren.

Forschungsfrage			Skala
Differenzen	Einfach zwei Gruppen Design	Unabhaengige Mittelwerte t-Test	Intervall Verhaeltnis
		Mann-Whitney U Test	Ordinal
		Chi-Quadrat Unabhaengigkeitstest	Nominal
	Pretest / Posttest Design	Abhaengige Stichproben t-Test	Intervall
		Wilcoxon oder Sign Test	Ordinal
		Mc Nemar Test	Nominal
	Zeitreihen Modelle	Zeitreihen Analyse	Intervall
	Kovarianz oder repeated measures Design	Repeated Measures ANOVA oder ANCOVA	Intervall
		Friedman’s ANOVA	Ordinal
		Cochran’s Q	Nominal
	Drei oder Mehrere Gruppen Design	ANOVA und MANOVA	Intervall
		Kruskal-Wallis ANOVA	Ordinal
		Chi-Quadrat Homogenitaetstest	Nominal
Deskriptive	Eine Variable, mit bekannte Grundgesamtheit	Mittelwert t-Test	Intervall
		Kolmogorov-Smirnof Anpassungstest	Ordinal
		Chi-Quadrat Anpassungstest	Nominal
Kausal oder Beziehung	Eine Stichprobe (Gruppe) mit zwei oder mehreren Variablen	Pearson’s korrelationskoeffizient, Bartlett’s Test	Intervall
		Spearman Rang Korrelation, Kendall’s Tau	Ordinal
		Lambda Beta, Chi-Quadrat Unabhaengigkeitstest	Nominal
		Phi-Korrelation, Fisher Exact Test	Dichotom